Aproximaciones a la Integral
La integración es la mejor manera de encontrar el área desde una curva hasta el eje x: obtenemos una fórmula para una respuesta exacta.
¡Pero la integración a veces puede ser difícil o imposible de hacer!
Pero no te preocupes, porque podemos sumar muchas porciones para
obtener una respuesta aproximada.
¡Vamos a ello!
Ejemplos
Sea f(x) = ln(x) de x = 1 a x = 4
De hecho, podemos integrar eso y obtener la verdadera respuesta de 2.54517744447956....
Pero imagina que no podemos, y lo único que podemos hacer es calcular los valores de ln(x):
- en x=1: ln(1) = 0
- en x=2: ln(2) = 0.693147...
- etc.
Usemos una porción rectangular de ancho igual a 1 para que sea más fácil ver lo que está pasando (pero las porciones más pequeñas son mejores).
Hay algunos métodos diferentes que podemos usar:
Suma Izquierda Rectangular de Riemann (SIRR)
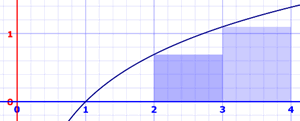
Este método usa rectángulos cuya altura es el valor más a la izquierda. Las áreas son:
- x=1 a 2: ln(1) × 1 = 0 × 1 = 0
- x=2 a 3: ln(2) × 1 = 0.693147... × 1 = 0.693147...
- x=3 a 4: ln(3) × 1 = 1.098612... × 1 = 1.098612...
Sumando estas nos da 1.791759, mucho menor que 2.545177. ¿Por
qué?
Porque nos falta toda esa área entre la parte superior de los
rectángulos y la curva.
Esto se ve aún más afectado por una curva que aumenta constantemente.
Cuando una curva sube y baja, el error suele ser menor.
Suma Derecha Rectangular de Riemann (SDRR)
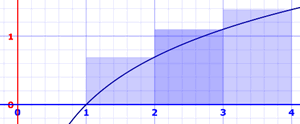
Ahora calculamos la altura del rectángulo usando el valor más a la derecha. Las áreas son:
- x=1 a 2: ln(2) × 1 = 0.693147... × 1 = 0.693147...
- x=2 a 3: ln(3) × 1 = 1.098612... × 1 = 1.098612...
- x=3 a 4: ln(4) × 1 = 1.386294... × 1 = 1.386294...
Sumando estas se obtiene 3.178054, que ahora es mucho más alto que 2.545177, porque hemos incluido áreas entre las partes superiores de los rectángulos y la curva.
Suma Punto Medio Rectangular de Riemann (SPMRR)
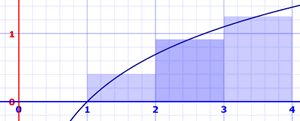
¡También podemos usar el punto medio! Las áreas son:
- x=1 a 2: ln(1.5) × 1 = 0.405465... × 1 = 0.405465...
- x=2 a 3: ln(2.5) × 1 = 0.916291... × 1 = 0.916291...
- x=3 a 4: ln(3.5) × 1 = 1.252763... × 1 = 1.252763...
Sumando estas, se obtiene 2.574519 ..., que está bastante cerca de 2.545177.
Regla Trapezoidal
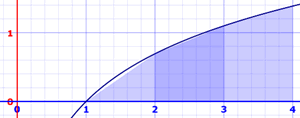
Podemos usar ambos lados para obtener una forma triangular en la parte superior, que suelen formar trapecios con la base de cada porción.
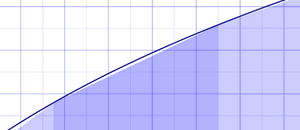
El cálculo simplemente promedia los valores izquierdo y derecho. Las áreas son:
- x=1 a 2: ln(1) + ln(2) 2 × 1 = 0 + 0.693147...2 × 1 = 0.346573...
- x=2 a 3: ln(2) + ln(3)2 × 1 = 0.693147... + 1.098612...2 × 1 = 0.895879...
- x=3 a 4: ln(3) + ln(4)2 × 1 = 1.098612... + 1.386294...2 × 1 = 1.242453...
Sumando estas se obtiene 2.484907, que todavía es un poco más bajo que 2.545177, principalmente porque la curva es cóncava hacia abajo en el intervalo dado.
Observa que en la práctica cada valor se usa dos veces (excepto el primero y el último) y luego la suma completa se divide por 2:
ln(1) + ln(2) 2 × 1 + ln(2) + ln(3) 2 × 1 + ln(3) + ln(4) 2 × 1
1 2 × ( ln(1) + ln(2) + ln(2) + ln(3) + ln(3) + ln(4) )
1 2 × ( ln(1) + 2 ln(2) + 2 ln(3) + ln(4) )
Entonces podemos tener una fórmula general:
Δx 2 × ( f(x0) + 2f(x1) + 2f(x2) + ... 2f(xn-1) + f(xn) )
Por cierto, este método es simplemente el promedio de los métodos por la izquierda y la derecha:
Aproximación Trapezoidal = SIRR + SDRR 2
Nota: los 4 métodos anteriores se denominan Sumas de Riemann en honor al matemático alemán Bernhard Riemann (1826 - 1866).
Regla de Simpson
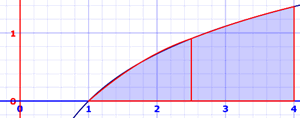
Una mejora de la Regla Trapezoidal es la Regla de Simpson. Se basa en utilizar parábolas en la parte superior en lugar de líneas rectas. Las parábolas a menudo se acercan bastante a la curva real:
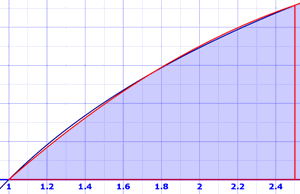
Suena difícil, pero terminamos con una fórmula como la fórmula del trapezoide (pero dividimos por 3 y usamos un patrón de factores 4,2,4,2,4):
Δx 3 × ( f(x0) + 4f(x1) + 2f(x2) + ... 4f(xn-1) + f(xn) )
Ojo: n debe ser par. Entonces, tomemos 6 porciones de 0.5 cada una:
0.5 3 × ( f(1) + 4f(1.5) + 2f(2) + 4f(2.5) + 2f(3) + 4f(3.5) + f(4) )
Evaluando toda la suma nos da:
0.5 3 × ( 15.2679... )
2.544648...
Este es un gran resultado en comparación a 2.545177....
Más y Menos
Cuando la curva está por debajo del eje, el valor de la integral es
negativo.
Entonces obtenemos un valor "neto".
Si queremos un área total (por ejemplo si quisiéramos pintarla)
podemos usar la función valor
absoluto abs(). O busca manualmente el punto dónde la
curva cruza el eje x, luego elabora integrales separadas e invierte
los negativos antes de sumar.
Error y Precisión
Comparemos los métodos
| f(x)=ln(x) | N = 3 | N = 6 | N = 100 | |||||
| Estimación | Error | Estimación | Error | Estimación | Error | |||
| SIRR | 1.791759 | 0.753418 | 2.183140 | 0.362037 | 2.524327 | 0.020850 | ||
| SDRR | 3.178054 | -0.632877 | 2.876287 | -0.331110 | 2.565916 | -0.020739 | ||
| SPMRR | 2.574519 | -0.029342 | 2.552851 | -0.007674 | 2.545206 | -0.000029 | ||
| Regla Trapezoidal | 2.484907 | 0.060271 | 2.529713 | 0.015464 | 2.545121 | 0.000055 | ||
| Regla de Simpson | (N debe ser par) | 2.544648 | 0.000529 | 2.545177 | <0.000001 | |||
¡La Regla de Simpson gana! Y es tan fácil de
usar como las demás.
Por supuesto, una función diferente producirá resultados diferentes.
¿Por qué no pruebas una tú mismo?
Error Máximo
En la práctica, no sabremos la respuesta real ... entonces, ¿cómo
sabemos qué tan buena es nuestra estimación?
Puedes obtener una buena sensación probando diferentes anchos para las
porciones.
Y también existen estas fórmulas para el error máximo
de aproximación (estas son para el peor de los casos, y el error real,
con suerte, será mucho menor):
Para Punto Medio: |E| = K(b-a)3 24n2
Para Trapezoidal: |E| = K(b-a)3 12n2
Para Simpson: |E| = M(b-a)5 180n4
Donde:
- |E| es el valor absoluto del error máximo (puede ser positivo o negativo)
- a es el comienzo del intervalo
- b es el final del intervalo
- n es el número de cortes
- K es la segunda derivada más grande del intervalo.
- M es la cuarta derivada más grande del intervalo.
(Por "mayor" nos referimos al valor absoluto máximo).
a, b y n son fáciles, pero ¿cómo encontramos K y M ?
Ejemplo: f(x) = ln(x) entre 1 y 4
Primero busquemos algunas derivadas, las necesitaremos:
- 1ra derivada: f'(x) = 1/x
- 2da derivada: f''(x) = −1/x2
- 3ra derivada: f(3)(x) = 2/x3
- 4ta derivada: f(4)(x) = −6/x4
- 5ta derivada: f(5)(x) = 24/x5
El valor más grande de K podría estar al principio, al final o en algún punto intermedio:
- Comienzo: f''(1) = −1/12 = −1
- Final: f''(4) = −1/42 = −1/16
- En medio: usa la 3ra derivada para ver si hay ceros
en el intervalo de 1 a 4, lo que podría significar un cambio de
dirección.
¿Hay algún valor entre 1 y 4 tal que f(3)(x) = 0? No. Entonces el máximo está al principio o al final.
Entonces K = 1 (el valor absoluto máximo)
Lo mismo para M, pero con derivadas más altas:
- Comienzo: f(4)(1) = −6/14 = −6
- Final: f(4)(4) = −6/44= −6/256
- En medio: usa la 5ta derivada para ver si hay ceros
en el intervalo de 1 a 4.
¿Hay algún valor entre 1 y 4 tal que f(5)(x) = 24/x5 es igual a cero? No.
Para solo 6 cortes, los errores máximos son:
Punto medio: |E| = 1(4-1)3 24×62 = 0.03125
Trapezoidal: |E| = 1(4-1)3 12×62 = 0.0625
Simpson: |E| = 6(4-1)5 180×64 = 0.00625
Formas conocidas
La curva puede tener una forma que conocemos y podemos usar fórmulas de geometría, como en estos ejemplos:
Ejemplo: Triángulo
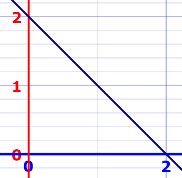
f(x) = 2 − x, de 0 a 2
A = ½ × 2 × 2 = 2
Ejemplo: Rectángulo
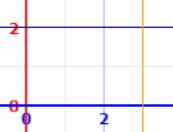
f(x) = 2, de 0 a 3
A = 2 × 3 = 6
Ejemplo: Semicírculo
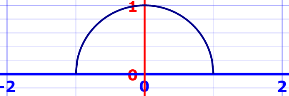
f(x) = √(1 − x2), de −1 a +1
A = π r2 / 2 = π / 2
Conclusión
Podemos estimar el área bajo una curva dividiendo una función
- Suma Izquierda Rectangular de Riemann (SIRR)
- Suma Derecha Rectangular de Riemann (SDRR)
- Suma Punto Medio Rectangular de Riemann (SPMRR)
- Regla Trapezoidal
- Regla de Simpson
