Desviación Estándar y Varianza
Desviación significa qué tan lejos de lo normal
Desviación Estándar
La Desviación Estándar es una medida de qué tan dispersos están los datos.
Su símbolo es σ (la letra griega sigma)
La fórmula es fácil: es la raíz cuadrada de la Varianza. Así que ahora te preguntarás: "¿Qué es la Varianza?"
Varianza
La Varianza se define como:
La media de las diferencias con la media elevadas al cuadrado.
Para calcular la varianza sigue estos pasos:
- Calcula la Media (el promedio simple de los números)
- Luego, para cada número: resta la Media y eleva el resultado al cuadrado (la diferencia al cuadrado)
- Luego calcula la media de esas diferencias al cuadrado. (¿Por qué al cuadrado?)
Ejemplo
Tú y tus amigos acaban de medir las alturas de sus perros (en milímetros):
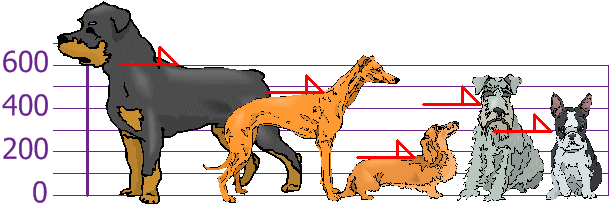
Las alturas (hasta los hombros) son: 600 mm, 470 mm, 170 mm, 430 mm y 300 mm.
Calcula la Media, la Varianza y la Desviación Estándar.
Tu primer paso es encontrar la Media:
Respuesta:
| Media | = | 600 + 470 + 170 + 430 + 3005 |
| = | 19705 | |
| = | 394 |
así que la altura media (promedio) es 394 mm. Vamos a dibujar esto en el gráfico:
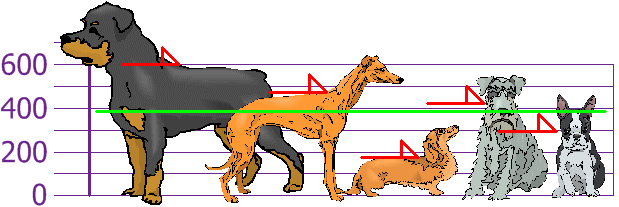
Ahora calculamos la diferencia de cada perro respecto a la Media:
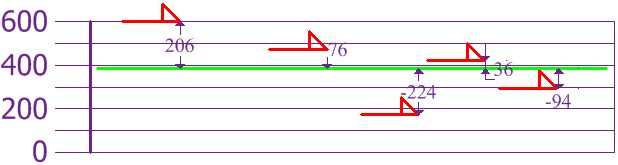
Para calcular la Varianza, toma cada diferencia, elévala al cuadrado, y luego calcula el promedio del resultado:
| Varianza | ||
| σ2 | = | 2062 + 762 + (−224)2 + 362 + (−94)25 |
| = | 42436 + 5776 + 50176 + 1296 + 88365 | |
| = | 1085205 | |
| = | 21704 | |
Así que la Varianza es 21,704
Y la Desviación Estándar es simplemente la raíz cuadrada de la Varianza, así que:
| Desviación Estándar | ||
| σ | = | √21704 |
| = | 147.32... | |
| = | 147 (al mm más cercano) | |
Nota: La Varianza usa unidades al cuadrado. Aquí es 21,704 mm2. Sacar la raíz cuadrada nos devuelve la Desviación Estándar en milímetros.
Lo bueno de la Desviación Estándar es que es útil. Ahora podemos mostrar qué alturas están dentro de una Desviación Estándar (147 mm) de la Media:
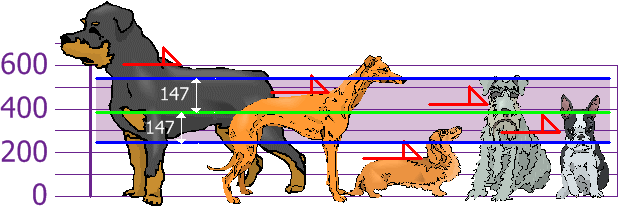
Así que, usando la Desviación Estándar tenemos una manera "estándar" de saber qué es normal, y qué es extra grande o extra pequeño.
Los Rottweilers son perros grandes. Y los Dachshunds son un poco pequeños, ¿verdad?
¿Por qué es útil?
Cuando los datos tienen forma de campana (normal):
- alrededor del 68% de los valores están dentro de 1 desviación estándar de la media
- y alrededor del 95% de los valores están dentro de 2 desviaciones estándar
Por lo tanto, da una muy buena idea de qué valores esperar.
Pero con datos sesgados o valores atípicos, estos porcentajes pueden ser muy diferentes.
Lee Distribución Normal Estándar para aprender más.
También prueba la Calculadora de Desviación Estándar.
Pero ... hay un pequeño cambio para los datos de una Muestra
Nuestro ejemplo ha sido para una Población (los 5 perros son los únicos perros que nos interesan).
Pero si los datos son una Muestra (una selección tomada de una Población más grande), ¡entonces el cálculo cambia!
Cuando tenemos N valores de datos que son:
- La Población: divide entre N al calcular la Varianza (como lo hicimos)
- Una Muestra: divide entre N−1 al calcular la Varianza
Todos los demás cálculos permanecen igual, incluida la forma en que calculamos la media.
Ejemplo: si nuestros 5 perros son solo una muestra de una población mayor de perros, dividimos entre 4 en lugar de 5 de esta manera:
Dividir entre N−1 en lugar de N se llama corrección de Bessel: da una varianza ligeramente mayor porque una muestra pequeña puede no mostrar toda la variación en la población.
Receta para la Desviación Estándar
- Encuentra la media
- Encuentra cada diferencia respecto a la media
- Eleva al cuadrado cada diferencia
- Calcula el promedio de los cuadrados: divide entre N (población) o N−1 (muestra)
- Saca la raíz cuadrada
Fórmulas
Aquí están las dos fórmulas, explicadas en Fórmulas de Desviación Estándar si quieres saber más:
|
La Desviación Estándar de la "Población": |
![raíz cuadrada de [ (1/N) por Sigma de i=1 a N de (xi - mu)^2 ]](images/standard-deviation-formula.svg) |
|
| La Desviación Estándar de la "Muestra": | ![raíz cuadrada de [ (1/(N-1)) por Sigma de i=1 a N de (xi - xbarra)^2 ]](images/standard-deviation-sample.svg) |
Parece complicado, pero el cambio importante es
dividir entre N−1 (en lugar de N) al calcular la Desviación Estándar de una Muestra.
*Nota al pie: ¿Por qué elevar al cuadrado las diferencias?
Si solo sumamos las diferencias de la media ... los negativos cancelan a los positivos:
 |
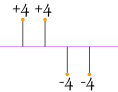4 + 4 − 4 − 44 = 0 |
Así que eso no funcionará. ¿Qué tal si usamos valores absolutos?
|
|4| + |4| + |−4| + |−4|4 = 4 + 4 + 4 + 44 = 4 |
Eso se ve bien (y es la Desviación Media), pero ¿qué tal este caso?
 |
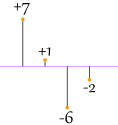|7| + |1| + |−6| + |−2|4 = 7 + 1 + 6 + 24 = 4 |
¡Oh, no! También da un valor de 4, a pesar de que las diferencias están más dispersas.
Así que intentemos elevar al cuadrado cada diferencia (y sacar la raíz cuadrada al final):
|
√(42 + 42 + (-4)2 + (-4)24) = √(644) = 4 | |
|
√(72 + 12 + (-6)2 + (-2)24) = √(904) = 4.74... |
¡Eso está genial! La Desviación Estándar es mayor cuando las diferencias están más dispersas ... justo lo que queremos.
De hecho, este método es una idea similar a la distancia entre puntos, solo que aplicado de una manera diferente.
Y es más fácil usar álgebra con cuadrados y raíces cuadradas que con valores absolutos, lo que hace que la desviación estándar sea fácil de usar en otras áreas de las matemáticas.