Variable Aleatoria - Continua
Una variable aleatoria es un conjunto de valores posibles de un experimento aleatorio.
Ejemplo: Al lanzar una moneda podríamos obtener Cara o Cruz.
Vamos a darles los valores Cara = 0 y Cruz = 1 y tenemos una variable aleatoria "X":
Usando notación matemática:
X = {0, 1}
Nota: ¡Podríamos elegir Cara = 100 y Cruz = 150 u otros valores si queremos! Es nuestra elección.
Continua
Las variables aleatorias pueden ser Discretas o Continuas:
- Los datos discretos solo pueden tomar ciertos valores (como 1,2,3,4,5)
- Los datos continuos pueden tomar cualquier valor dentro de un rango (como la altura de una persona)
En nuestra Introducción a la Variable
Aleatoria (¡por favor lee eso primero!) miramos muchos ejemplos
de variables aleatorias discretas.
Pero aquí vemos el tema más avanzado de Variables Aleatorias
Continuas.
Distribución uniforme
La distribución uniforme (también llamada distribución rectangular) es la distribución más simple.Todos los valores de la variable aleatoria entre a y b tienen la misma probabilidad:
La probabilidad de cualquier valor entre a y b es p
También sabemos que p = 1 / (b−a), porque el total de todas las probabilidades debe ser 1, entonces
Podemos escribir:
P(X = x) = 1/(b−a) para todo a ≤
x ≤ b
P(X = x) = 0 en cualquier otro valor

Ejemplo: El géiser "Viejo Fiel" (Old Faithful) entra en erupción cada 91 minutos. Llegas al azar y esperas 20 minutos ... ¿cuál es la probabilidad de que lo veas estallar?
Esto es realmente fácil de calcular, 20 minutos de 91 minutos son:
p = 20/91 = 0.22 (a 2 decimales)
Pero usemos la Distribución Uniforme para practicar.
Para encontrar la probabilidad entre a y a + 20, encuentra el área azul:
Área = (1/91) x (a+20 − a)
= (1/91) x 20
= 20/91
= 0.22 (a 2 decimales)
Si esperas los 91 minutos completos, estarías seguro (p=1) de haberlo visto erupcionar.
¡Pero recuerda que esto es algo al azar! Podría entrar en erupción en el momento de tu llegada, o en cualquier momento en los 91 minutos.
Distribución uniforme acumulada
Podemos tener la distribución uniforme como una distribución acumulada (sumando a medida que avanza):
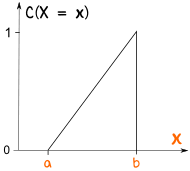
La probabilidad comienza en 0 y aumenta hasta 1
Este tipo de cosas se denomina "Función de Distribución Acumulada", a menudo abreviada a "FDA" o "FD"
Ejemplo (continuación):
Usemos la "FDA" de la Distribución Uniforme anterior para calcular la probabilidad:
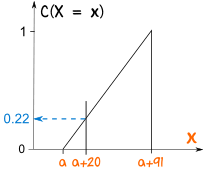
En a + 20 la probabilidad se ha acumulado a aproximadamente 0.22
Otras distribuciones
| Saber cómo usar la Distribución Uniforme ayuda cuando se trata de distribuciones más complicadas como esta: |
El nombre general de cualquiera de estas es función de densidad de probabilidad o "FDP" o "PDF" en inglés (no tiene que ver con el formato de archivo del mismo nombre).
La distribución normal
La distribución continua más importante es la Distribución Normal Estándar
Es muy importante que la Variable Aleatoria tenga su propia letra especial Z.La gráfica para Z es una curva simétrica en forma de campana:
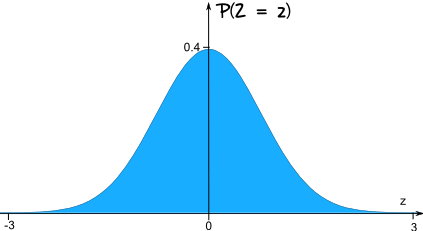
Por lo general, queremos encontrar la probabilidad de que Z esté entre ciertos valores.
Ejemplo: P(0 < Z < 0.45)
(¿Cuál es la probabilidad de que Z esté entre 0 y 0.45?)
Esto se encuentra usando la Tabla
de Distribución Normal Estándar
Comienza en la fila de 0.4 y sigue leyendo hasta 0.45: ahí está el valor 0.1736
P(0 < Z < 0.45) = 0.1736
Resumen
- Una Variable Aleatoria es una variable cuyos valores posibles son resultados numéricos de un experimento aleatorio.
- Las Variables Aleatorias pueden ser discretas o continuas.
- Un ejemplo importante de una Variable Aleatoria continua es la variable Normal Estándar, Z.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
