División larga - Adivinar con puntería
Entonces, ¿cómo funciona la división larga? Funciona partiendo el número grande y haciendo cada trozo por separado.
Miles, cientos, ...
Para verlo, vamos a intentar adivinar la respuesta de 7,698 ÷ 6, pero con un método especial.
Empezamos por los millares, después las centenas, después las decenas, después las unidades.
OK, empezamos por los miles: ¿Cuántos 6 bloques de mil caben en 7,698? Bueno, uno solo. Dos serían demasiado:
| 1,000 x 6 = 6,000 | demasiado pequeño |
| 2,000 x 6 = 12,000 | demasiado grande |
Hemos avanzado un poco. Ahora podemos adivinar que la respuesta está entre 1,000 y 2,000.
Pasamos a las centenas. Sumamos centenas de una en una:
| 1,100 x 6 = 6,600 | demasiado pequeño |
| 1,200 x 6 = 7,200 | demasiado pequeño |
| 1,300 x 6 = 7,800 | demasiado grande |
Entonces, está entre 1,200 y 1,300. Vamos con las decenas:
| 1,210 x 6 = 7,260 | demasiado pequeño |
| 1,220 x 6 = 7,320 | demasiado pequeño |
| 1,230 x 6 = ... |
¡Stop! Se va a hacer muy largo con tanta multiplicación...
... debería de haber una manera más fácil...
Volvamos atrás:
Ya sabemos que 1,200 bloques de 6 está cerca, así que por qué no reducir 7,698 en esa cantidad:
7,698 − 6 × 1,200 = 7,698 − 7,200 = 498 que nos quedan por resolver
Mejor así, ¡el problema es más fácil cuanto más lo trabajas!
¿Dónde estábamos? Eso es, con las decenas, pero ahora con el número 498:
| 10 x 6 = 60 | demasiado pequeño |
| 20 x 6 = 120 | demasiado pequeño |
| ... | |
| 80 x 6 = 480 | demasiado pequeño |
| 90 x 6 = 540 | demasiado grande |
Entonces, 8 bloques de diez.
Podemos volver a reducir el problema:
498 − 480 = 18 quedan por resolver
| 1 x 6 = 6 | demasiado pequeño |
| 2 x 6 = 12 | demasiado pequeño |
| 3 x 6 = 18 | ¡BINGO! |
Lo hemos conseguido. Ahora tenemos un millar, 2 centenas, 8 decenas y 3 unidades = 1,283.
Pero mejor lo comprobamos:
|
1,283 x 6 = 7,698 ... ¡SÍ!
|
La moraleja de la historia es:
No trabajes todo el tiempo con el número completo,
trabaja sólo con lo que te queda por adivinar.
Vamos a probarlo otra vez, sin entretenernos:
Empezamos con 7,698
| Millares | 1,000 x 6 = 6,000 | demasiado pequeño |
| 2,000 x 6 = 12,000 | demasiado grande |
Así que los millares son 1,000 x 6.
7,698 − 1,000 x 6 = 1,698 que nos quedan por averiguar:
| Centenas | 100 x 6 = 600 | demasiado pequeño |
| 200 x 6 = 1,200 | demasiado pequeño | |
| 300 x 6 = 1,800 | demasiado grande |
Así que las centenas son 200 x 6.
1,698 − 200 x 6 = 1,698 − 1,200 = 498 que nos quedan por averiguar
| Decenas | 80 x 6 = 480 | demasiado pequeño |
| 90 x 6 = 540 | demasiado grande |
Y la respuesta de las decenas es 80 x 6.
498 − 80 x 6 = 498 − 480 = 18 que faltan
| Unidades | 3 x 6 = 18 | ¡perfecto! |
Entonces las unidades dan 3 x 6.
El resultado: 1,000 x 6 + 200 x 6 + 80 x 6 + 3 x 6 = 7,698, ¡y la respuesta es 1,283!
Pero no hacen falta tantas palabras, podemos escribirlo así:
|
Lo que hicimos:
|
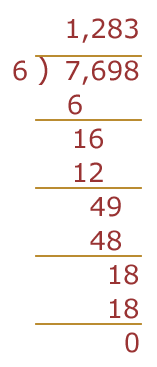
Cómo lo escribiremos:
|
|
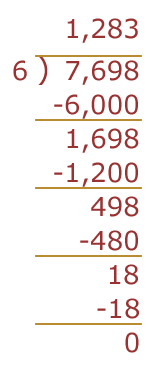 |
|
 |
Siguiente: División larga >>>

