Lanzar una moneda a una cuadrícula

Hace unos cientos de años, a la gente le gustaba apostar arrojando monedas al suelo: ¿la moneda cruzaría una línea o no?
Un hombre (Georges-Louis Leclerc, el conde de Buffon, lee La aguja de Buffon) empezó a pensar en esto y calculó la probabilidad.
Se llama "Aguja de Buffon" en su honor.
¡Ahora es tu turno de probar!
Necesitarás:
 |
Una pequeña moneda redonda, como 1 centavo estadounidense, 1 centavo de un euro o 50
centavos mexicanos. |
 |
Una hoja de papel con líneas separadas por 30 mm. |
Pasos
- Mide el diámetro de tu moneda: ____ mm
- Por ejemplo: un centavo estadounidense es de 19 mm, un euro de 1 centavo es de 16.25 mm.
- Mide también el espaciado de su cuadrícula (puede que no se imprima exactamente a 30 mm): ____ mm
- Coloca tu hoja de papel sobre una superficie plana, como la superficie de una mesa o el piso.
- Desde una altura de unos 5 cm, deja caer la moneda sobre el papel y registra si cae:
-
A: Completamente dentro de un cuadrado
(sin tocar ninguna línea de cuadrícula)B: Cruza una o más líneas

La altura exacta desde la que dejas caer la moneda no es importante, ¡pero no la dejes tan cerca del papel que estás engañando!
Si la moneda sale completamente del papel, no cuentes ese turno.
100 veces
Ahora soltaremos la moneda 100 veces, pero primero ...
... ¿Qué porcentaje crees que aterrizará A o B?
Haz una suposición (estimación) antes de comenzar el experimento:
| Tu estimación para "A" (%): | |
| Tu estimación para "B" (%): |
Bien, comencemos.
Suelta la moneda 100 veces y registra A (no toca una línea) o B (toca o cruza una línea) usando las Marcas de conteo:
| La moneda cae | Cuenta | Frecuencia | Porcentaje |
|
A
|
|||
|
B
|
|||
| Totales: | 100 | 100% |
Ahora dibuja una Gráfica de barras para ilustrar tus resultados.
Puedes crear uno en Gráficas de datos (barra, línea y pastel).
- ¿Las barras tienen la misma altura?
- ¿Esperabas que lo fueran
- ¿Cómo se compara el resultado con tu suposición?
Podemos calcular lo que debería ser ...
Aquí hay algunas posiciones para que la moneda aterrice de modo que no toque una de las líneas:
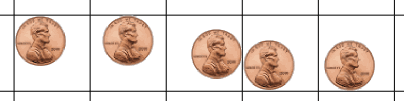
Coloca tu moneda en su cuadrícula (como arriba), y luego pon una marca en el papel donde está el centro de la moneda (solo una estimación aproximada será suficiente).
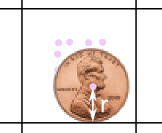 |
Mira cómo el centro de la moneda está a un radio r de una línea. (Lee sobre el Radio y diámetro del círculo) |
Haz muchas "marcas centrales" y luego dibuja un cuadro que las conecte todas como se muestra a continuación:
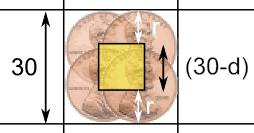
d = diámetro de la moneda (2 × r)
Cuando el centro de una moneda está dentro del cuadro amarillo, no tocará ninguna línea.
La caja amarilla es más pequeña que la cuadrícula por dos radios (= un diámetro) de la moneda.
Entonces, ¿cuáles son las áreas?
- El área del cuadrado de la cuadrícula es 30 × 30 = 900 mm2
- El área del cuadro amarillo es (30-d) × (30-d) = (30-d)2 mm2
El cálculo anterior fue para una cuadrícula de 30 mm, pero podemos usar S para el tamaño de la cuadrícula:
- El área del cuadrado de la cuadrícula es S × S = S2 mm2
- El área del recuadro amarillo es (S-d)2 mm2
Ejemplo: 1c de Euro (d = 16.25 mm) en una cuadrícula de 29 mm (S = 29 mm):
Cuadrado de la cuadrícula = 292 = 841 mm2
Caja amarilla = (29-16.25)2 = 12.752 = 162 mm2 (redondeado a mm2)
Por lo tanto, debes esperar que la moneda aterrice sin cruzar una línea de la cuadrícula aproximadamente:
"A" = 162 / 841 = 19.3% de las veces
Y "B" = 100% - 19.3% = 80.7%
Ahora haz los cálculos para tu propio tamaño de cuadrícula y tamaño de moneda.
| Espaciado de cuadrícula S (mm): | |
| Diámetro de la moneda d (mm): | |
| Área del cuadrado de la cuadrícula = S2 (mm2): | |
| Área del recuadro amarillo = (S-d)2 (mm2): | |
| "A" (%): | |
| "B" (%): |
¿Cómo se comparan estos resultados teóricos con sus resultados experimentales?
No será exacto (porque es algo aleatorio) pero puede estar cerca.
Diferentes tamaños de moneda
Intenta repetir el experimento con una moneda de diferente tamaño.
- Primero calcula el valor teórico ... ¿cómo afecta esto a los valores de A y B?
- Luego, haz el experimento para ver qué tan cerca estás.
Qué has hecho
- Te has divertido (con suerte) realizando un experimento.
- Has hecho algo de geometría y tienes algo de experiencia en el cálculo de áreas y probabilidades.
- Y has visto la relación entre teoría y realidad.
