Actividad: Subconjuntos
¡Lee primero Introducción a Conjuntos!
En esta actividad investigarás cuántos subconjuntos tiene un conjunto.
¿Qué es un subconjunto?
Un subconjunto es un conjunto contenido en otro conjunto.
Es como si pudieras elegir helado de los siguientes sabores:
{plátano, chocolate, vainilla}
Puedes elegir cualquier sabor {plátano}, {chocolate} o {vainilla},
O cualquiera de los dos sabores: {plátano, chocolate}, {plátano, vainilla} o {chocolate, vainilla}.
O los tres sabores (no tiene nada de malo),
O podrías decir "ninguno en absoluto, gracias", que es el "conjunto vacío": {}
Ejemplo: El conjunto {alex, brenda, carlos, delia}
Tiene los subconjuntos:
- {alex}
- {brenda}
- etc...
También tiene los subconjuntos:
- {alex, brenda}
- {alex, carlos}
- {brenda, delia}
- etc...
También:
- {alex, brenda, carlos}
- {alex, brenda, delia}
- etc...
Y también:
- todo el conjunto: {alex, brenda, carlos, delia}
- el conjunto vacío: {}
Ahora comencemos con el Conjunto Vacío y sigamos hacia arriba...
El conjunto vacío
¿Cuántos subconjuntos tiene el conjunto vacío?
Podrías elegir:
- todo el conjunto: {}
- el conjunto vacío: {}
Pero, espera un minuto, ¡en este caso son lo mismo!
Entonces, el conjunto vacío realmente tiene solo 1 subconjunto (que es en sí mismo, el conjunto vacío).
Es como preguntar "No hay nada disponible, entonces, ¿qué eliges?" Responde "nada". Esa es tu única opción. Bien.
Un conjunto con un elemento
El conjunto podría ser cualquier cosa, pero digamos que es:
{manzana}
¿Cuántos subconjuntos tiene el conjunto {manzana}?
- todo el conjunto: {manzana}
- el conjunto vacío: {}
Y eso es todo. Puedes elegir un elemento o nada.
Entonces cualquier conjunto con un elemento tendrá 2 subconjuntos.
Un conjunto con dos elementos
Agreguemos otro elemento a nuestro conjunto de ejemplo:
{manzana, plátano}
¿Cuántos subconjuntos tiene el conjunto {manzana, plátano}?
Podrías tener {manzana}, o {plátano}, y no olvides:
- el conjunto completo: {manzana, plátano}
- el conjunto vacío: {}
Entonces un conjunto con dos elementos tiene 4 subconjuntos.
Un conjunto con tres elementos
Qué tal si:
{manzana, plátano, cereza}
Bien, seamos más sistemáticos ahora y listemos los subconjuntos por cuántos elementos tienen:
Subconjuntos con un elemento: {manzana}, {plátano}, {cereza}
Subconjuntos con dos elementos: {manzana, plátano}, {manzana, cereza}, {plátano, cereza}
Y:
- el conjunto completo: {manzana, plátano, cereza}
- el conjunto vacío: {}
De hecho lo podríamos poner en una tabla:
| Lista | Número de subconjuntos |
|
| cero elementos | {} | 1 |
| un elemento | {manzana}, {plátano}, {cereza} | 3 |
| dos elementos | {manzana, plátano}, {manzana, cereza}, {plátano, cereza} | 3 |
| tres elementos | {manzana, plátano, cereza} | 1 |
| Total: | 8 | |
(Nota: ¿viste un patrón en los números anteriores?)
Conjuntos con cuatro elementos (¡tu turno!)
Ahora intenta hacer lo mismo para este conjunto:
{manzana, plátano, cereza, dátil}
Aquí hay una tabla para ti:
| Lista | Número de subconjuntos |
|
| cero elementos | {} | |
| un elemento | ||
| dos elementos | ||
| tres elementos | ||
| cuatro elementos | ||
| Total: | ||
(Nota: si lo hiciste bien, habrá un patrón en los números).
Conjuntos con cinco elementos
Y ahora:
{manzana, plátano, cereza, dátil, fresa}
Aquí hay una tabla para ti:
| Lista | Número de subconjuntos |
|
| cero elementos | {} | |
| un elemento | ||
| dos elementos | ||
| tres elementos | ||
| cuatro elementos | ||
| cinco elementos | ||
| Total: | ||
(¿Había un patrón en los números?)
Conjuntos con seis elementos
Qué pasa:
{manzana, plátano, cereza, dátil, fresa, naranja}
OK... no necesitamos completar una tabla, porque...
Duplicación
Lo primero que debe notar es que el número total de subconjuntos se duplica cada vez:
Un conjunto de n elementos tiene 2n subconjuntos
Entonces deberías poder responder:
- ¿Cuántos subconjuntos hay para un conjunto de 6 elementos? _____
- ¿Cuántos subconjuntos hay para un conjunto de 7 elementos? _____
Otro patrón
Ahora pensemos en subconjuntos y tamaños:
- El conjunto vacío tiene solo 1 subconjunto: 1
- Un conjunto con un elemento tiene 1 subconjunto sin elementos y 1 subconjunto con un elemento: 1 1
- Un conjunto con dos elementos tiene 1 subconjunto sin elementos, 2 subconjuntos con un elemento y 1 subconjunto con dos elementos: 1 2 1
- Un conjunto con tres elementos tiene 1 subconjunto sin elementos, 3 subconjuntos con un elemento, 3 subconjuntos con dos elementos y 1 subconjunto con tres elementos: 1 3 3 1
- ¡y así!
¿Reconoces este patrón de números?
¡Son los números del Triángulo de Pascal!
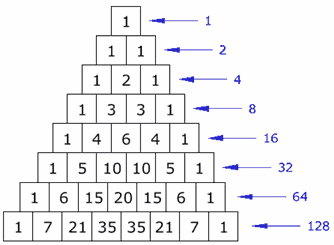
Esto es muy útil, porque ahora puedes verificar si tienes la cantidad correcta de subconjuntos.
Nota: las filas comienzan en 0, al igual que las columnas.
Ejemplo: para el conjunto {manzana, plátano, cereza, dátil, fresa} enumera subconjuntos de longitud tres:
- {manzana, plátano, cereza}
- {manzana, plátano, dátil}
- {manzana, plátano, fresa}
- {manzana, cereza, fresa}
Pero eso es solo 4 subconjuntos, ¿cuántos debería haber?
Bueno, estás eligiendo 3 de 5, así que ve a la fila 5, posición 3 del Triángulo de Pascal (recuerda comenzar a contar desde 0) para encontrar que necesitas 10 subconjuntos, ¡así que debes pensar más!
De hecho, estos son los resultados: {manzana, plátano, cereza}, {manzana, plátano, dátil}, {manzana, plátano, fresa}, {manzana, cereza, dátil} , {manzana, cereza, fresa}, {manzana, dátil, fresa}, {plátano, cereza, dátil}, {plátano, cereza, fresa}, {plátano, dátil, fresa}, {cereza, dátil, fresa}
Calcular los números
¿Hay alguna forma de calcular los números como 1, 4, 6, 4 y 1 (en lugar de buscarlos en el Triángulo de Pascal)?
Sí, podemos encontrar el número de formas de seleccionar cada número de elementos usando Combinaciones.
Hay cuatro elementos en el conjunto, por lo tanto:
- Número de formas de seleccionar 0 elementos de 4 = 4C0 = 1
- Número de formas de seleccionar 1 elemento de 4 = 4C1 = 4
- Número de formas de seleccionar 2 elementos de 4 = 4C2 = 6
- Número de formas de seleccionar 3 elementos de 4 = 4C3 = 4
- Número de formas de seleccionar 4 elementos de 4 = 4C4 = 1
- Número total de subconjuntos = 16
¿Puedes hacer lo mismo con un conjunto de cinco elementos?
Completa lo siguiente:
- Número de formas de seleccionar 0 elementos de 5 = 5C0 = 1
- Número de formas de seleccionar 1 elemento de 5 = ___________
- Número de formas de seleccionar 2 elementos de 5 = ___________
- Número de formas de seleccionar 3 elementos de 5 = ___________
- Número de formas de seleccionar 4 elementos de 5 = ___________
- Número de formas de seleccionar 5 elementos de 5 = ___________
- Número total de subconjuntos = ___________
Conclusión
En esta actividad:
- Descubriste una regla para determinar el número total de subconjuntos para un conjunto dado: Un conjunto con n elementos tiene 2n subconjuntos.
- Encontraste una conexión entre los números de subconjuntos de cada tamaño con los números en el triángulo de Pascal.
- Descubriste una forma rápida de calcular estos números usando Combinaciones.
Más importante aún, has aprendido cómo se pueden combinar diferentes ramas de las matemáticas.
