Usando Exponentes y Logaritmos

¿Qué es un exponente?

El exponente de un número dice cuántas veces
usar el número en una multiplicación.

En este ejemplo: 2³ = 2 × 2 × 2 = 8

(el 2 se usa 3 veces en una multiplicación para obtener 8)

¿Qué es un logaritmo?

Los Logaritmos funcionan al revés.

Hace la pregunta "¿qué exponente produjo esto?":

2^? = 8

Y lo responde así:

exponente a logaritmo

En este ejemplo:

El exponente toma 2 y 3 y da 8 (2, usado 3 veces en una multiplicación, da 8)
El logaritmo toma 2 y 8 y da 3 (el 2 da 8 cuando se usa 3 veces en una multiplicación)

Un logaritmo dice cuántos de un mismo número se multiplican para obtener otro número

Entonces, un logaritmo realmente te da el exponente como respuesta:

concepto de logaritmo

(Mira también como Exponentes, Raíces y Logaritmos están relacionados.)

Trabajando juntos

Los exponentes y los logaritmos funcionan bien juntos porque se "deshacen" entre sí (siempre que la base "a" sea la misma):

Exponente vs Logaritmo

Son "Funciones Inversas"

Calcular uno, luego el otro, te lleva de regreso a donde comenzaste:

Calcular a^x, luego log_a, da x de nuevo:

Calcular log_a, luego a^x, da x de nuevo:

Es una pena que estén escritos de manera tan diferente ... hace que las cosas se vean extrañas. Por lo tanto, puede ayudar pensar en a^x como "arriba" y log_a(x) como "abajo":

ir para arriba y luego para abajo, te devuelve de nuevo:abajo(arriba(x)) = x

ir para abajo y luego ir para arriba, te devuelve de nuevo:arriba(abajo(x)) = x

De todos modos, lo importante es que:

La función logarítmica se "deshace" por la función exponencial.

(y viceversa)

Como en este ejemplo:

Ejemplo: ¿Cuánto vale x en log₃(x) = 5?

Empieza con:log₃(x) = 5

Queremos "deshacer" el log₃ para quedarnos con "x ="

Usa la Función Exponencial (de ambos lados):

Y sabemos que

, así que:x = 3⁵

Respuesta: x = 243

Y también:

Ejemplo: Calcula el valor de y en y=log₄(1/4)

Empieza con:y = log₄(1/4)

Usa la función exponencial de ambos lados:

Simplifica:4^y = 1/4

Un truquito: 1/4 = 4⁻¹

Entonces:4^y = 4⁻¹

Finalmente:y = −1

Propiedades de los logaritmos

Una de las cosas poderosas sobre los logaritmos es que pueden convertir la multiplicación en suma.

log_a( m × n ) = log_am + log_an

"el logaritmo de una multiplicación es la suma de los logaritmos"

¿Por qué es eso cierto? Ver nota al pie.

Usando esa propiedad y las Leyes de los Exponentes obtenemos estas propiedades útiles:

log_a(m × n) = log_am + log_an	el logaritmo de una multiplicación es la suma de los logaritmos

log_a(m/n) = log_am − log_an	el logaritmo de una división es la resta de los logaritmos

log_a(1/n) = −log_an	esto solo sigue la regla de "división" anterior, porque log_a(1) = 0

log_a(m^r) = r ( log_am )	el logaritmo de m elevado a la r es r veces el logaritmo de m

Recuerda: ¡la base "a" es siempre la misma!

libro de logaritmos Historia: los logaritmos eran muy útiles antes de que se inventaran las calculadoras ... por ejemplo, en lugar de multiplicar dos números grandes, usando logaritmos podría convertirlo en una suma (¡mucho más fácil!)

Y había libros llenos de tablas de Logaritmos para ayudar.

Divirtámonos usando las propiedades:

Ejemplo: Simplifica log_a( (x²+1)⁴√x )

Empieza con:log_a( (x²+1)⁴√x )

Usa log_a(mn) = log_am + log_an :log_a( (x²+1)⁴ ) + log_a( √x )

Usa log_a(m^r) = r ( log_am ) : 4 log_a(x²+1) + log_a( √x )

También √x = x^½ :4 log_a(x²+1) + log_a( x^½ )

Usa log_a(m^r) = r ( log_am ) otra vez: 4 log_a(x²+1) + ½ log_a(x)

Eso es todo lo que podemos simplificar ... no podemos hacer nada con log_a(x²+1).

Respuesta: 4 log_a(x²+1) + ½ log_a(x)

Nota: no hay una regla para manejar log_a(m+n) ni log_a(m−n)

También podemos aplicar las reglas de logaritmo "al revés" para combinar logaritmos:

Ejemplo: Convierta esto en un logaritmo: log_a(5) + log_a(x) − log_a(2)

Empieza con:log_a(5) + log_a(x) − log_a(2)

Usa log_a(mn) = log_am + log_an :log_a(5x) − log_a(2)

Usa log_a(m/n) = log_am − log_an : log_a(5x/2)

Respuesta: log_a(5x/2)

El logaritmo natural y las funciones exponenciales naturales

Cuando la base es e ("Número de Euler" = 2.718281828459...) tenemos:

El logaritmo natural log_e(x) que se escribe más comúnmente ln(x)
La función exponencial natural (o función exponencial continua) e^x

Y la misma idea de que uno puede "deshacer" al otro sigue siendo cierta:

ln(e^x) = x

e^{(ln x)} = x

Y aquí están sus gráficas:

Natural Logarithm		Función Exponencial Natural

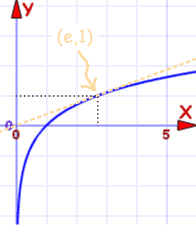
Gráfica de f(x) = ln(x)		Gráfica de f(x) = e^x
Pasa por (1,0) y (e,1)		Pasa por (0,1) y (1,e)

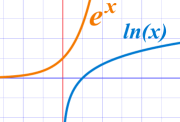
ln(x) vs e^x

Son la misma curva con los ejes x y y invertidos.

Lo cual es otra manera para mostrar que son funciones inversas.

En una calculadora, el logaritmo natural es el botón "ln".

Siempre trata de usar logaritmos naturales y la función exponencial natural siempre que sea posible.

El logaritmo común

Cuando la base es 10 se tiene:

El logaritmo común log₁₀(x), que se suele escribir como log(x)

A los ingenieros les encanta usarlo, pero no se usa mucho en matemáticas.

En una calculadora, el logaritmo común es el botón "log".

Es útil porque te dice qué tan "grande" es el número en el sistema decimal (cuántas veces necesitas usar 10 en una multiplicación).

Ejemplo: Calcula log₁₀ 100

Bueno, 10 × 10 = 100, así que cuando el 10 se usa 2 veces en una multiplicación se obtiene 100:

log₁₀ 100 = 2

Del mismo modo, log₁₀ 1,000 = 3, log₁₀ 10,000 = 4, y así sucesivamente.

Ejemplo: Calcula log₁₀ 369

OK, lo mejor es usar el botón "log" de la calculadora:

log₁₀ 369 = 2.567...

Cambio de Base

¿Qué pasa si queremos cambiar la base de un logaritmo?

¡Fácil! Solo usa esta fórmula:

Cambio de Base Logaritmo

"x va arriba, a va abajo"

Otra forma de pensar es que log_b a es como un "factor de conversión" (la misma fórmula que la anterior):

log_a x = log_b x / log_b a

Entonces ahora podemos convertir de cualquier base a cualquier otra base.

Otra propiedad útil es:

log_a x = 1 / log_x a

¿Ves cómo "x" y "a" intercambian posiciones?

Ejemplo: Calcula 1 / log₈ 2

1 / log₈ 2 = log₂ 8

Y 2 × 2 × 2 = 8, así que cuando el 2 se usa 3 veces en una multiplicación se obtiene 8:

1 / log₈ 2 = log₂ 8 = 3

Pero usamos el logaritmo natural con más frecuencia, por lo que vale la pena recordar esto:

log_a x = ln x / ln a

Ejemplo: Calcula log₄ 22

Mi calculadora no tiene un botón "log₄" ...

... pero sí que tiene un botón "ln", y podemos usarlo:

log₄ 22 = ln 22 / ln 4

= 3.09.../1.39...

= 2.23 (a 2 decimales)

¿Qué significa esta respuesta? Significa que 4 con un exponente de 2.23 es igual a 22. Entonces podemos verificar esa respuesta:

Comprobación: 4^2.23 = 22.01 (¡suficientemente cerca!)

Aquí hay otro ejemplo:

Ejemplo: Calcula log₅ 125

log₅ 125 = ln 125 / ln 5

= 4.83.../1.61...

=3 (exactamente)

Yo sé que 5 × 5 × 5 = 125, (5 se usa 3 veces para obtener 125), así que esperaba que la respuesta fuera 3, ¡y funcionó!

Uso en el mundo real

Estos son algunos usos de los logaritmos en el mundo real:

Terremotos

La magnitud de un terremoto es una escala logarítmica.

La famosa "Escala de Richter" utiliza esta fórmula:

M = log₁₀ A + B

Donde A es la amplitud (en mm) medida por el Sismógrafo
y B es un factor de corrección de distancia

Hoy en día hay fórmulas más complicadas, pero igualmente usan una escala logarítmica.

Sonido

El volumen se mide en decibelios (dB para abreviar):

Volumen en dB = 10 log₁₀ (p × 10¹²)

donde p es la presión del sonido.

Ácido o alcalino

La acidez (o alcalinidad) se mide en pH:

pH = −log₁₀ [H⁺]

donde H⁺ es la concentración molar de iones de hidrógeno disueltos.
Nota: en química [ ] significa concentración molar (moles por litro).

Más ejemplos

Ejemplo: Resuelve 2 log₈ x = log₈ 16

Empieza con:2 log₈ x = log₈ 16

Pon el "2" dentro del log:log₈ x² = log₈ 16

Quita los logs (son de la misma base): x² = 16

Resuelve:x = −4 ó +4

Pero ... pero ... pero ... ¡no puedes tener un logaritmo de un número negativo!

Entonces el caso −4 no está definido.

Respuesta: 4

Verifica: usa tu calculadora para ver si ésta es la respuesta correcta ... también prueba el caso "−4".

Ejemplo: Resuelve e^−w = e^2w+6

Empieza con:e^−w = e^2w+6

Aplica ln de ambos lados:ln(e^−w) = ln(e^2w+6)

Y ln(e^w)=w: −w = 2w+6

Simplifica:−3w = 6

Resuelve:w = 6/−3 = −2

Respuesta: w = −2

Comprobación: e⁻⁽⁻²⁾= e² y e^2(−2)+6=e²

Nota al pie: ¿Por qué log(m × n) = log(m) + log(n) ?

Para ver porqué, usaremos y :

Primero, convierta m y n en "exponentes de logaritmos":

Luego usa las Leyes de Exponentes

Finalmente deshaz los exponentes.

Es una de esas cosas inteligentes que hacemos en matemáticas que se puede describir como "no podemos hacerlo aquí, así que vamos allá, hagámoslo y luego volvemos".

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).