Resolver Triángulos LLA
"LLA" significa "Lado, Lado, Ángulo"
|
"LLA" es cuando conocemos dos lados y un ángulo que no es el ángulo entre los lados. |
|
Para resolver un triángulo LLA
|
Ejemplo 1
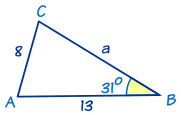
En este triángulo conocemos:
- ángulo B = 31°
- b = 8
- y c = 13
En este caso, podemos usar primero La Ley de Senos para hallar el ángulo C:
A continuación podemos usar que los tres ángulos suman 180° para hallar el ángulo A:
Ahora podemos usar La Ley de los Senos nuevamente para encontrar:
Observa que no usamos A = 92.2°, ese ángulo se redondeó a 1 decimal. Es mucho mejor usar el número no redondeado 92.181 ...° que aún debería estar en nuestra calculadora desde el último cálculo.
Entonces, hemos resuelto completamente el triángulo ...
... ¿o falta algo?
*En el ejemplo, cuando calculamos:
C = sin−1(0.8369...)
C = 56.818...°
No consideramos que sin−1(0.8369...) podría tener dos respuestas (lee La Ley de Senos)
La otra posible respuesta para C es 180° − 56.818...°
Aquí puedes ver por qué tenemos dos posibles respuestas:
Al girar el lado "8" hacia la izquierda y hacia la
derecha podemos
unirlo con el lado "a" en dos ubicaciones posibles.
A esto se le conoce como un caso ambiguo.
Así que volvamos y continuemos con nuestro ejemplo:
El otro ángulo posible es:
Usa que "los tres ángulos suman 180 °" para encontrar el ángulo A:
Ahora podemos usar La Ley de los Senos nuevamente para encontrar:
Entonces los dos conjuntos de respuestas son:
C = 56.8°, A = 92.2°, a = 15.52
C = 123.2°, A = 25.8°, a = 6.76
Ejemplo 2
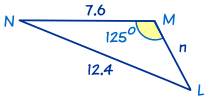
En este triángulo conocemos el ángulo M = 125°, m = 12.4 y l = 7.6
Primeramente, usaremos la Ley de Senos para encontrar el ángulo L:
Ahora usaremos que "los tres ángulos suman 180°" para encontrar el ángulo N:
Y ahora podemos usar La Ley de los Senos nuevamente para encontrar:
Nota que solo hay una respuesta en este caso. El lado que mide "12.4" solo une un lugar.
La otra respuesta posible para L es 149.9°. Pero eso es imposible porque ya tenemos M=125° y un triángulo no puede tener dos ángulos mayores que 90°.
Ejemplo 3: ¿¡Pero qué...!?
- ángulo A = 35°
- lado a = 4
- lado c = 9
¡Espera! El seno de un ángulo nunca puede ser mayor que 1. Esto significa que no existe tal triángulo.
Conclusión:
Al resolver un triángulo "Lado,
Lado, Ángulo"
¡necesitamos comprobar si podría haber otra respuesta válida!
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
