Teoremas, Corolarios y Lemas
¿Qué son todas esas cosas? ¡Suenan tan impresionantes!
Bueno, son básicamente hechos: algunos resultados a los que se ha llegado.
- Un Teorema es un resultado importante
- Un Corolario es un teorema que sigue de otro teorema.
- Un Lema es un resultado pequeño (menos importante que un teorema)
Ejemplos
Aquí hay un ejemplo de Geometría:
Ejemplo: un teorema y un corolario
Teorema:
Los ángulos de un lado de una línea recta siempre suman 180°.
Corolario:
Siguiendo con ese teorema, encontramos que donde dos líneas se cruzan, los ángulos opuestos entre sí (llamados Opuestos por el Vértice) son iguales (a=c y b=d en el diagrama).
Ángulo a = Ángulo
c
Ángulo b = Ángulo
d
Demostración:
Los ángulos a y b suman 180° porque están del mismo lado de una línea:
a + b = 180°
a = 180° − b
Del mismo modo para los ángulos b y c
b + c = 180°
c = 180° − b
Y dado que a y c son iguales a 180° − b, entonces
a = c
Y un ejemplo un poco más complicado de Geometría:
Ejemplo: un teorema, un corolario y también un lema.
Teorema:
Un ángulo inscrito a° mide la mitad del ángulo central 2a°
Esto se llama Teorema
del Ángulo Central.
Demostración: Une el centro O al punto A.
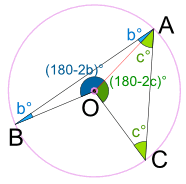
El triángulo ABO es isósceles (dos lados iguales, dos ángulos iguales), entonces:
Y, usando que los Ángulos internos de un Triángulo suman 180°:
El triángulo ACO es isósceles, entonces:
Y, de nuevo, usando que los Ángulos internos de un Triángulo suman 180°:
Y, usando que los Ángulos alrededor de un punto suman 360°:
Reemplaza b + c con a, y se tiene:
Ángulo BAC = a° y Ángulo BOC = 2a°
(Ese fue un resultado "importante", por lo que es un Teorema).
Corolario
(Esto se llama "Teorema de los Ángulos con el Mismo Arco", pero en realidad es solo un Corolario del "Teorema del Ángulo Central")
Manteniendo los puntos extremos fijos ... ... el ángulo a° siempre mide lo mismo, sin importar dónde se encuentre en la circunferencia:
Entonces, los Ángulos subtendidos por el mismo arco son iguales.
Lema
(Esto a veces se llama el "Teorema del Ángulo en el Semicírculo", pero en realidad es solo un Lema al "Teorema del Ángulo Central")
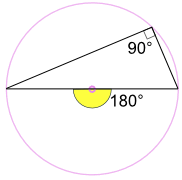
En el caso especial donde el ángulo central forma un diámetro del círculo:
2a° = 180° , por lo que a° = 90°
Entonces, un ángulo inscrito en un semicírculo es siempre un ángulo recto.(Ese fue un resultado "pequeño", así que es un Lema).
Otro ejemplo, relacionado con el Teorema de Pitágoras:
Ejemplo:
Teorema
Si m y n son dos números enteros tales que:
- a = m2 − n2
- b = 2mn
- c = m2 + n2
entonces a2 + b2 = c2
Demostración:
(Ese fue un resultado "importante").
Corolario
a, b y c, tal como se definieron arriba, son una Terna Pitagórica
Demostración:
Del Teorema sabemos que a2 + b2
= c2,
Entonces a, b y c son una Terna Pitagórica
(Ese resultado "siguió" del Teorema anterior).
Lema
Si m = 2 y n = 1, entonces obtenemos la terna pitagórica 3, 4 y 5
Demostración:
Si m = 2 y n = 1, entonces
- a = 22 − 12 = 4 − 1 = 3
- b = 2 × 2 × 1 = 4
- c = 22 + 12 = 4 + 1 = 5
(Ese fue un resultado "pequeño").




