Resolver Triángulos LAL
"LAL" significa "Lado, Ángulo, Lado"
|
"LAL" es cuando conocemos dos lados y el ángulo entre ellos. |
Para resolver un triángulo LAL
- usa La Ley de Cosenos para hallar el lado desconocido,
- luego usa La Ley de Senos para encontrar el más pequeño de los otros dos ángulos,
- usa que los tres ángulos suman 180° para hallar el último ángulo
Ejemplo 1
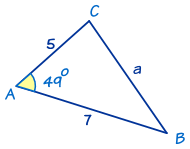
En este triángulo conocemos:
- ángulo A = 49°
- lado b = 5, y
- lado c = 7
Para resolver el triángulo necesitamos encontrar el lado a y los ángulos B y C.
Usa la Ley de los Cosenos para encontrar primero el lado a:
a2 = b2 + c2 − 2bc cosA
Ahora usamos la Ley de los Senos para encontrar el más pequeño de los otros dos ángulos.
Elegimos el ángulo B:
sin Bb = sin Aa
Ahora hallamos el ángulo C, lo cual es fácil usando 'los ángulos de un triángulo suman 180°':
Ahora hemos resuelto el triángulo por completo... hemos encontrado todos sus ángulos y lados.
Ejemplo 2
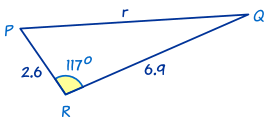
Este también es un triángulo LAL.
Primero busquemos r usando la Ley de los Cosenos:
r2 = p2 + q2 − 2pq cos R
Ahora vamos con la Ley de los Senos.
¿Elegir el ángulo más pequeño? ¡No es necesario! El ángulo R es mayor de 90°, por lo que los ángulos P y Q deben ser menores de 90° obligatoriamente.
sin Pp = sin Rr
Finalmente hallaremos el ángulo Q usando 'los ángulos de un triángulo suman 180°':
¡Todo terminado!
Dominar esta habilidad necesita mucha práctica, así que ...
¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).
