Media, Mediana y Moda en Frecuencias Agrupadas

Explicadas con Tres Ejemplos

La carrera y el cachorro travieso

Esto comienza con algunos datos sin procesar (aún no es hay frecuencias agrupadas) ...

corredores

Alex cronometró a 21 personas en la carrera de velocidad, redondeando al segundo más cercano:

59, 65, 61, 62, 53, 55, 60, 70, 64, 56, 58, 58, 62, 62, 68, 65, 56, 59, 68, 61, 67

Para encontrar la Media Alex suma todos los números, luego divide entre la cantidad de números:

Media = 59 + 65 + 61 + 62 + 53 + 55 + 60 + 70 + 64 + 56 + 58 + 58 + 62 + 62 + 68 + 65 + 56 + 59 + 68 + 61 + 6721
Mean = 61.38095...

Para encontrar la Mediana Alex coloca los números en orden de menor a mayor y encuentra el número del medio.

frecuencia

En este caso la mediana es el 11^er número:

53, 55, 56, 56, 58, 58, 59, 59, 60, 61, 61, 62, 62, 62, 64, 65, 65, 67, 68, 68, 70

Mediana = 61

Para encontrar la Moda, o valor modal, Alex coloca los números en orden de menor a mayor y luego cuenta cuántos hay de cada número. La moda es el número que aparece con más frecuencia (puede haber más de una moda):

53, 55, 56, 56, 58, 58, 59, 59, 60, 61, 61, 62, 62, 62, 64, 65, 65, 67, 68, 68, 70

62 aparece tres veces, más a menudo que los otros valores, entonces Moda = 62

Tabla de Frecuencias Agrupadas

A continuación, Alex hace una Tabla de Frecuencias Agrupadas:

Segundos	Frecuencia
51 - 55	2
56 - 60	7
61 - 65	8
66 - 70	4

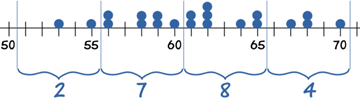
frecuencia con clases

Entonces 2 corredores tardaron entre 51 y 55 segundos, 7 tomaron entre 56 y 60 segundos, etc.

¡Oh No!

De repente, todos los datos originales se pierden (cachorro travieso)

Solo la Tabla de Frecuencias Agrupadas sobrevivió ...

... ¿podemos ayudar a Alex a calcular la media, la mediana y la moda solo con esa tabla?

La respuesta es ... no, no podemos. No de forma exacta. Pero, podemos hacer estimaciones.

Estimación de la media a partir de datos agrupados

Entonces todo lo que nos queda es:

Segundos	Frecuencia
51 - 55	2
56 - 60	7
61 - 65	8
66 - 70	4

Los grupos (51-55, 56-60, etc.), también llamados clases, son de ancho (o tamaño) 5

Los puntos medios están en el medio de cada clase: 53, 58, 63 y 68

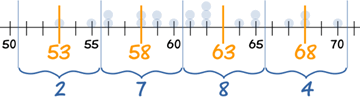
frecuencias agrupadas

Podemos estimar la media usando los puntos medios.

¿Entonces, cómo funciona esto?

Piensa en los 7 corredores de la clase 56 - 60: todo lo que sabemos es que corrieron entre 56 y 60 segundos:

Tal vez los siete hicieron 56 segundos,
Tal vez los siete hicieron 60 segundos,
Pero es más probable que haya una dispersión de números: algunos a 56, otros a 57, etc.

Entonces tomamos un promedio y asumimos que los siete tomaron 58 segundos.

Ahora hagamos la tabla usando puntos medios:

Punto Medio	Frecuencia
53	2
58	7
63	8
68	4

frecuencias agrupadas

Nuestro pensamiento es: "2 personas tardaron 53 segundos, 7 personas tardaron 58 segundos, 8 personas tardaron 63 segundos y 4 tardaron 68 segundos". En otras palabras, imaginamos que los datos se ven así:

53, 53, 58, 58, 58, 58, 58, 58, 58, 63, 63, 63, 63, 63, 63, 63, 63, 68, 68, 68, 68

Luego los sumamos todos y dividimos entre 21. La forma rápida de hacerlo es multiplicar cada punto medio por cada frecuencia:

Punto medio x	Frecuencia f	Punto medio × Frecuencia fx
53	2	106
58	7	406
63	8	504
68	4	272
Totales:	21	1288

Y luego, nuestra estimación del tiempo medio para completar la carrera es:

Media Estimada = 128821 = 61.333...

Muy cerca de la respuesta exacta que obtuvimos antes.

Estimación de la mediana a partir de datos agrupados

Miremos nuestros datos nuevamente:

Segundos	Frecuencia
51 - 55	2
56 - 60	7
61 - 65	8
66 - 70	4

frecuencias agrupadas

La mediana es el valor medio, que en nuestro caso es el 11^ero, que está en la clase 61 - 65:

Podemos decir "la clase de la mediana es 61 - 65"

Pero si queremos un valor estimado para la mediana, debemos mirar más de cerca la clase 61 - 65.

Lo llamamos "61 - 65", pero realmente incluye valores desde 60.5 hasta (pero sin incluir) 65.5.

¿Por qué? Bueno, los valores están en segundos completos, por lo que un tiempo real de 60.5 se mide como 61. Del mismo modo, 65.4 se mide como 65.

En 60.5 ya tenemos 9 corredores, y para el próximo límite en 65.5 tenemos 17 corredores. Al dibujar una línea recta en el medio, podemos determinar dónde está la frecuencia mediana de n/2 corredores:

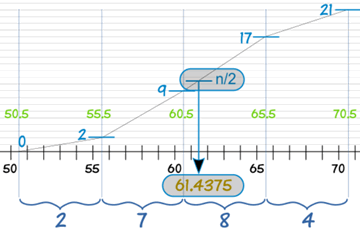
frecuencias agrupadas

Y esta práctica fórmula hace el cálculo:

Mediana Estimada = I + (n/2) − QM × A

donde:

I es el límite inferior de la clase que contiene la mediana
n es el número total de valores
Q es la frecuencia acumulada de las clases antes de la clase de la mediana
M es la frecuencia de la clase de la mediana
A es el ancho de la clase

Para nuestro ejemplo:

I = 60.5
n = 21
Q = 2 + 7 = 9
M = 8
A = 5

Mediana Estimada= 60.5 + (21/2) − 9 8 × 5

= 60.5 + 0.9375

= 61.4375

Estimación de la moda a partir de datos agrupados

Miremos nuestros datos nuevamente:

Segundos	Frecuencia
51 - 55	2
56 - 60	7
61 - 65	8
66 - 70	4

Podemos encontrar fácilmente la clase modal (la clase con la frecuencia más alta), que es 61 - 65

Podemos decir "la clase modal es 61 - 65"

¡Pero la moda real puede que ni siquiera esté en ese grupo! O puede haber más de una moda. Sin los datos sin procesar no sabremos realmente.

Pero, podemos estimar la moda usando la siguiente fórmula:

Moda Estimada = I + f_m − f_m-1(f_m − f_m-1) + (f_m − f_m+1) × A

donde:

I es el límite inferior de la clase modal
f_m-1 es la frecuencia de la clase que está antes de la clase modal
f_m es la frecuencia de la clase modal
f_m+1 es la frecuencia de la clase que está después de la clase modal
A es el ancho de la clase

Para nuestro ejemplo:

I = 60.5
f_m-1 = 7
f_m = 8
f_m+1 = 4
A = 5

Moda Estimada= 60.5 + 8 − 7(8 − 7) + (8 − 4) × 5

= 60.5 + (1/5) × 5

= 61.5

Nuestos resultados finales son:

Media Estimada: 61.333...
Mediana Estimada: 61.4375
Moda Estimada: 61.5

(Compara eso con la verdadera media, mediana y moda de 61.38 ..., 61 y 62 que obtuvimos al principio).

Y así es como se hace.

¡Ahora echemos un vistazo a dos ejemplos más y practiquemos un poco más en el camino!

Ejemplo de zanahorias "baby"

carrots

Ejemplo: Cultivaste cincuenta zanahorias baby usando tierra de cultivo especial. Las desentierras y mides sus longitudes (redondeando al mm más cercano) y agrupas los resultados:

Longitud (mm)	Frecuencia
150 - 154	5
155 - 159	2
160 - 164	6
165 - 169	8
170 - 174	9
175 - 179	11
180 - 184	6
185 - 189	3

Media

Longitud (mm)	Punto medio x	Frecuencia f	fx
150 - 154	152	5	760
155 - 159	157	2	314
160 - 164	162	6	972
165 - 169	167	8	1336
170 - 174	172	9	1548
175 - 179	177	11	1947
180 - 184	182	6	1092
185 - 189	187	3	561
	Totales:	50	8530

Media Estimada = 853050 = 170.6 mm

Mediana

La mediana es la media de la longitud 25^ta y 26^ta, por lo que está en la clase 170 - 174:

I = 169.5 (el límite inferior de la clase 170-174)
n = 50
Q = 5 + 2 + 6 + 8 = 21
M = 9
A = 5

Mediana Estimada= 169.5 + (50/2) − 219 × 5

= 169.5 + 2.22...

= 171.7 mm (a 1 decimal)

Moda

La clase modal es la que tiene la frecuencia más alta, que es 175 - 179:

I = 174.5 (el límite inferior de la clase 175 - 179)
f_m-1 = 9
f_m = 11
f_m+1 = 6
A = 5

Moda Estimada= 174.5 + 11 − 9(11 − 9) + (11 − 6) × 5

= 174.5 + 1.42...

= 175.9 mm (a 1 decimal)

Ejemplo con edades

La edad es un caso especial.

Cuando decimos "Sara tiene 17 años", ella permanece "17" hasta los dieciocho años.
Ella podría tener 17 años y 364 días y todavía estar clasificada como "17".

Esto cambia los puntos medios y los límites de la clase.

isla tropical

Ejemplo: las edades de las 112 personas que viven en una isla tropical se agrupan de la siguiente manera:

Edad	Frecuencia
0 - 9	20
10 - 19	21
20 - 29	23
30 - 39	16
40 - 49	11
50 - 59	10
60 - 69	7
70 - 79	3
80 - 89	1

Un niño en el primer grupo de 0 a 9 años podría tener casi 10 años. Entonces el punto medio para este grupo es 5, no 4.5

Los puntos medios son 5, 15, 25, 35, 45, 55, 65, 75 y 85

Del mismo modo, en los cálculos de mediana y moda, usaremos los límites de clase 0, 10, 20, etc.

Media

Edad	Punto medio x	Frecuencia f	fx
0 - 9	5	20	100
10 - 19	15	21	315
20 - 29	25	23	575
30 - 39	35	16	560
40 - 49	45	11	495
50 - 59	55	10	550
60 - 69	65	7	455
70 - 79	75	3	225
80 - 89	85	1	85
	Totales:	112	3360

Media Estimada = 3360112 = 30

Mediana

La mediana es la media de las edades de las personas 56^ta y 57^ma, por lo que está en la clase 20 - 29:

I = 20 (el límite inferior de la clase que contiene a la mediana)
n = 112
Q = 20 + 21 = 41
M = 23
A = 10

Mediana Estimada= 20 + (112/2) − 4123 × 10

= 20 + 6.52...

= 26.5 (a 1 decimal)

Moda

La clase modal es la que tiene la frecuencia más alta, que es 20 - 29:

I = 20 (el límite inferior de la clase modal)
f_m-1 = 21
f_m = 23
f_m+1 = 16
A = 10

Moda Estimada= 20 + 23 − 21(23 − 21) + (23 − 16) × 10

= 20 + 2.22...

= 22.2 (a 1 decimal)

Resumen

Para los datos agrupados, no podemos encontrar los valores exactos de la media, la mediana y la moda, solo podemos dar estimaciones.
Para estimar la media, usa los puntos medios de los intervalos de clase:
Media Estimada = Suma de (Punto medio × Frecuencia)Suma de Frecuencias
Para estimar la mediana, usa:
Mediana Estimada = I + (n/2) − QM × A

donde:
- I es el límite inferior de la clase que contiene la mediana
- n es el número total de valores
- Q es la frecuencia acumulada de las clases antes de la clase de la mediana
- M es la frecuencia de la clase de la mediana
- A es el ancho de la clase
Para estimar la moda, usa:
Moda Estimada = I + f_m − f_m-1(f_m − f_m-1) + (f_m − f_m+1) × A

donde:
- I es el límite inferior de la clase modal
- f_m-1 es la frecuencia de la clase que está antes de la clase modal
- f_m es la frecuencia de la clase modal
- f_m+1 es la frecuencia de la clase que está después de la clase modal
- A es el ancho de la clase

¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).