Exponentes
 |
El exponente de un número nos dice cuántas veces se usa el número en una multiplicación. En este ejemplo: 82 = 8 × 8 = 64
Los exponentes también se llaman potencias o índices |
Más ejemplos:
Ejemplo: 53 = 5 × 5 × 5 = 125
- En palabras: 53 se puede leer "5 a la tercera potencia", "5 a la potencia 3" o simplemente "5 al cubo"
Ejemplo: 24 = 2 × 2 × 2 × 2 = 16
- En palabras: 24 se puede leer "2 a la cuarta potencia" o "2 a la potencia 4" o simplemente "2 a la cuarta"
Y los exponentes hacen más fácil escribir muchas multiplicaciones
Ejemplo: 96 es más fácil de escribir y leer que 9 × 9 × 9 × 9 × 9 × 9
Puedes multiplicar cualquier número por sí mismo tantas veces como quieras con esta notación.
Haz la prueba aquí:
En general
| an
te dice que multipliques a por sí mismo, y hay n de esos a's: |
 |
Otra forma de escribirlo
A veces, la gente usa el símbolo ^ (arriba del 6 en su teclado), ya que es fácil de escribir.
Ejemplo: 2^4 es lo mismo que 24
- 2^4 = 2 × 2 × 2 × 2 = 16
Exponentes negativos
¿Negativos? ¿Qué es lo contrario de multiplicar? ¡Dividir!
Entonces dividimos por el número cada vez, que es lo mismo que multiplicar por 1número
Ejemplo: 8-1 = 18 = 0.125
O varias divisiones:
Ejemplo: 5-3 = 15 × 15 × 15 = 0.008
Pero esto lo podemos hacer más fácilmente:
5-3 también se puede calcular así:
15 × 5 × 5 = 153 = 1125 = 0.008
¿Negativo? Voltea y hazlo positivo
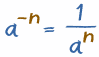 |
Este último ejemplo nos muestra una manera más fácil de manejar exponentes negativos:
|
Más ejemplos:
| Exponente negativo | Recíproco del exponente positivo | Respuesta | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0.0625 |
| 10-3 | = | 1 / 103 | = | 1/1,000 = 0.001 |
| (-2)-3 | = | 1 / (-2)3 | = | 1/(-8) = -0.125 |
¿Qué pasa si el exponente es 1 o 0?
| 1 | Si el exponente es 1, entonces tienes el número solo (por ejemplo 91 = 9) | |
| 0 | Si el exponente es 0, la respuesta es 1 (por ejemplo 90 = 1) | |
| ¿Pero qué hay de 00 ? Podría ser 1 o 0, por lo que la gente dice que es "indeterminado". |
Tiene sentido
Si miras esta tabla, verás que los exponentes positivos, cero y negativos son en realidad parte de un mismo (y bastante sencillo) patrón.
| Ejemplo: potencias de 5 | |||
|---|---|---|---|
| ... etc... |  |
||
| 52 | 1 × 5 × 5 | 25 | |
| 51 | 1 × 5 | 5 | |
| 50 | 1 | 1 | |
| 5-1 | 15 | 0.2 | |
| 5-2 | 15 × 15 | 0.04 | |
| ... etc... | |||
Ten cuidado a la hora de agrupar
Para evitar confusiones, usa paréntesis () en casos como estos:
| Con () : | (-2)2 = (-2) × (-2) = 4 |
| Sin () : | -22 = -(22) = - (2 × 2) = -4 |
| Con () : | (ab)2 = ab × ab |
| Sin () : | ab2 = a × (b)2 = a × b × b |
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
