Sistema binario de números
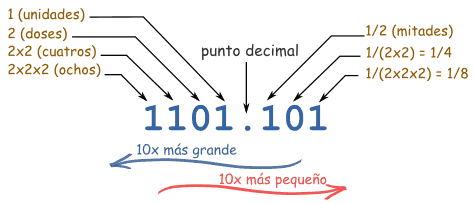 |
| Este número es 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8) (=13.625 en decimal) |
De la misma manera que en el sistema decimal, se pueden poner números a la izquierda o a la derecha del punto decimal, para indicar valores mayores o menores que uno. En el sistema binario:
| El número justo a la izquierda del punto es un número entero, lo llamamos unidades. Cuando vamos a la izquierda, cada posición vale 2 veces más. |
|
| La primera cifra a la derecha del punto significa mitades (1/2). Cuando vamos a la derecha, cada posición vale 2 veces menos (la mitad de la anterior). |
Dos valores diferentes
Como sólo puedes tener ceros y unos, en binario se cuenta así:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Binario: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
"El binario es tan fácil como 1, 10, 11."
Aquí tienes más equivalencias:
| Decimal: | 20 | 25 | 30 | 40 | 50 | 100 | 200 | 500 |
|---|---|---|---|---|---|---|---|---|
| Binario: | 10100 | 11001 | 11110 | 101000 | 110010 | 1100100 | 11001000 | 111110100 |
Definición de binario
|
La palabra binario viene de "bi-" que significa dos. Tenemos "bi-" en otras palabras como "bicicleta" (dos ruedas) o "binoculares" (dos ojos). |
|
|
Cuando leas un número binario, pronuncia cada dígito (por ejemplo, el número binario "101" se lee "uno cero uno"). De esta manera la gente no los confunde con números decimales. |
Bits
Un dígito binario por sí solo (como "0" o "1") se llama un "bit". Por ejemplo 11010 tiene cinco bits de longitud.
La palabra bit viene de las palabras inglesas "binary digit"
Cómo indicar que un número está en binario
Para mostrar que un número es binario, ponemos un pequeño 2 detrás: 1012
De esta manera nadie pensará que es el número decimal "101" (ciento uno).
Ejemplos
Ejemplo 1: ¿Cuánto es 11112 en decimal?
- El "1" de la izquierda está en la posición "2×2×2", esto es 1×2×2×2 (=8)
- El siguiente "1" está en la posición "2×2", esto es 1×2×2 (=4)
- El siguiente "1" está en la posición "2", esto es 1×2 (=2)
- El último "1" son las unidades, es decir 1
- Respuesta: 1111 = 8+4+2+1 = 15 en decimal
Ejemplo 2: ¿Cuánto es 10012 en decimal?
- El "1" de la izquierda está en la posición "2×2×2", así que vale 1×2×2×2 (=8)
- El "0" siguiente está en la posición "2×2", así que vale 0×2×2 (=0)
- El "0" está en la posición "2", así que vale 0×2 (=0)
- El último "1" son las unidades, así que vale 1
- Respuesta: 1001 = 8+0+0+1 = 9 en decimal
Ejemplo 3: ¿Cuánto es 1.12 en decimal?
- El "1" de la izquierda está en la posición de las unidades, así que vale 1.
- El "1" de la derecha está en la posición de las "mitades", así que vale 1×(1/2)
- Por tanto, 1.1 es igual a "1 y 1 medio" = 1.5 en decimal
Ejemplo 4: ¿Cuánto es 10.112 en decimal?
- El primer "1" está en la posición "2", así que vale 1×2 (=2)
- El "0" está en la posición de las unidades, vale 0
- El "1" a la derecha del punto está en la posición de las "mitades", así que vale 1×(1/2)
- El último "1" está en la posición de los "cuartos", así que vale 1×(1/4)
- Entonces, 10.11 es 2+0+1/2+1/4 = 2.75 en decimal
"Hay 10 tipos de personas en el mundo,
los que saben binario y los que no."
