Números imaginarios
| Un número que cuando se eleva al cuadrado da un resultado negativo. |
Vamos a probar a elevar algunos números al cuadrado a ver si podemos sacar un resultado negativo:
¡No hay suerte! Siempre positivo, o cero.
Parece que no podemos multiplicar un número por sí solo para obtener una respuesta negativa ...

Pero imagina que hay un número (vamos a llamarlo i de imaginario) que cumpliera esto:
¿Sería útil, qué podríamos hacer con él?
Comenzamos definiendo el número i como la raíz cuadrada de −1:
Esto nos permite trabajar con raíces cuadradas de números negativos de manera consistente.
Y eso es muy útil porque......simplemente aceptando que exista i podemos resolver muchos problemas donde nos hace falta la raíz cuadrada de un número negativo.
Ejemplo: Resolver x2 + 9 = 0
Podemos resolverlo paso a paso:
Debido a que definimos i como √−1, ahora podemos hacer esto:
Así, los números imaginarios nos ayudan a resolver ecuaciones que los números reales por sí solos no pueden.
También notemos que la raíz cuadrada de −9 es simplemente la raíz cuadrada de +9 (=3) multiplicada por i.
Esta regla funciona para cualquier número positivo x:
√(−x) = i√x
Mientras tengamos esa pequeña "i" ahí para recordarnos que hay que multiplicar por √−1 no tendremos problemas con seguir calculando para llegar a la solución.
Usando i
Ejemplo: ¿Cuánto es (5i)2 ?
Unidad imaginaria

La "unidad" imaginaria (el equivalente al 1 de los números reales) es √(−1) (la raíz cuadrada de menos uno).
En matemáticas el símbolo para √(−1) es i (de imaginario)
Pero en electrónica se usa j (porque "i" representa la corriente, y la letra siguiente después de la i es la j).Ejemplos de números imaginarios
| i | 12.38i | −i | 3i/4 | 0.01i | πi |
Los números imaginarios no son "imaginarios"
De hecho hubo un tiempo en que se pensó que los números imaginarios eran imposibles, y por eso se llamaban "imaginarios" (a modo de broma).
Pero después hubo gente que investigó más y descubrió que son útiles e importantes porque rellenan un hueco en matemáticas... pero el nombre de "imaginario" se mantuvo.
Y así es como surgió el nombre de los "números reales" (porque real no es imaginario).
Los números imaginarios son útiles
Los números imaginarios fueron introducidos por primera vez por los matemáticos en el siglo XVI para resolver ecuaciones que parecían imposibles. Hoy en día, se utilizan en todo, desde el diseño de aviones hasta la creación de efectos especiales en películas.
Números complejos
Los números imaginarios se vuelven más útiles cuando se combinan con números reales para formar números complejos como 3+5i o 6−4i
Analizador de espectro

¿Has visto esas pantallas geniales que hay cuando suena música? Sí, ¡se utilizan números complejos para los cálculos! Usando algo llamado "Transformadas de Fourier".
De hecho, se pueden hacer muchas cosas sofisticadas con el sonido
usando números complejos, como filtrar sonidos, escuchar susurros en
una multitud, etc.
Es parte de un área denominada "Procesamiento de señales".
Electricidad

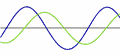
La CA o AC (corriente alterna) cambia de positivo a negativo siguiendo una onda sinuoidal.
Si combinas dos corrientes alternas puede que no coincidan bien, y puede ser muy difícil calcular la nueva corriente.
Pero usar números reales e imaginarios juntos hace mucho más fáciles los cálculos.
Y el resultado puede ser corriente "imaginaria", ¡pero puede hacerte daño igual!

Conjunto de Mandelbrot
El fascinante Conjunto de Mandelbrot (parte de él se muestra aquí) se basa en números complejos.
Ecuación cuadrática
Una ecuación cuadrática puede dar resultados con números imaginarios...
También la ciencia, la mecánica cuántica y la relatividad utilizan números complejos.
Propiedad interesante
La unidad imaginaria, i, tiene una propiedad interesante. "Da la vuelta" pasando por 4 valores diferentes cuando la multiplicas:
|
|||||||||||||||||
Por lo que tenemos esto:
| i = √−1 | i2 = −1 | i3 = −√−1 | i4 = +1 |
| i5 = √−1 | i6 = −1 | ...etc |
Ejemplo: ¿Cuánto es i10 ?
Y eso nos lleva a otro tema, el plano complejo:
Conclusión
- La unidad imaginaria, i, es igual a la raíz cuadrada de menos 1
- Nos ayudan a resolver ecuaciones que los números reales no pueden resolver.
- Se utilizan en ingeniería, física y arte.
- Al combinarse con números reales, forman números complejos.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).


