Teorema de Pitágoras
Pitágoras
Hace más de dos mil años, se descubrió un hecho asombroso sobre triángulos:
Si el triángulo tiene un ángulo recto (90°)...
... y pones un cuadrado sobre cada uno de sus lados, entonces...
... ¡el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos!
Se llama "Teorema de Pitágoras" y se puede escribir en una pequeña ecuación:
a2 + b2 = c2
Nota:
- c es el lado más largo del triángulo
- a y b son los otros dos lados
Definición
El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:
En un triángulo rectángulo:
el cuadrado de la hipotenusa es igual a
la suma de los cuadrados de los otros dos lados.
¿Seguro... ?
Veamos si funciona con un ejemplo.Ejemplo: Un triángulo "3,4,5" tiene un ángulo recto.
 |
Veamos si las áreas son las mismas: 32 + 42 = 52 Calculando obtenemos: 9 + 16 = 25 ¡sí, funciona! |

¿Por qué es útil esto?
Si sabemos las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos ayuda a encontrar la longitud del tercer lado. (¡Pero recuerda que solo funciona en triángulos rectángulos!)
¿Cómo lo uso?
Escríbelo como una ecuación: |
a2 + b2 = c2 |
Ahora puedes usar álgebra para
encontrar el valor que falta, como en estos ejemplos:
Ejemplo: Resuelve este triángulo
También puedes leer sobre Cuadrados y Raíces Cuadradas para ver porqué √169 = 13
Ejemplo: Resuelve este triángulo.
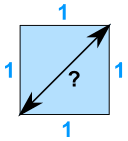
Ejemplo: ¿Cuál es la distancia diagonal a través de un cuadrado de tamaño 1?
También funciona al revés: cuando los tres lados de un triángulo cumplen que a2 + b2 = c2, entonces el triángulo tiene un ángulo recto.
Ejemplo: ¿Este triángulo tiene un ángulo recto?
¿Se cumple a2 + b2 = c2 ?
- a2 + b2 = 102 + 242 = 100 + 576 = 676
- c2 = 262 = 676
Son iguales, entonces ...
¡Sí, tiene un ángulo recto!
Ejemplo: ¿Un triángulo de 8, 15, 16 tiene un ángulo recto?
¿Se cumple 82 + 152 = 162 ?
- 82 + 152 = 64 + 225 = 289,
- pero 162 = 256
Entonces, NO, no tiene ángulo recto.
Ejemplo: ¿Este triángulo tiene un ángulo recto?
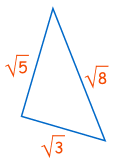
¿Se cumple a2 + b2 = c2 ?
¡Sí!
Entonces este es un triángulo rectángulo
¡Y tú mismo puedes demostrar el teorema!
Consigue papel, lápiz y tijeras, luego usa la siguiente animación como guía:
- Dibuja un triángulo rectángulo en el papel, dejando mucho espacio alrededor.
- Dibuja un cuadrado sobre la hipotenusa (el lado más largo)
- Dibuja un cuadrado del mismo tamaño en el otro lado de la hipotenusa
- Dibuja líneas como en la animación, así:

- Recorta los trozos
- Colócalos de manera que puedas demostrar que el cuadrado grande tiene la misma área que los cuadrados en los otros lados juntos
Otra Demostración, Muy Simple
Aquí tienes una de las demostraciones más antiguas de que el cuadrado grande tiene la misma área que los otros cuadrados juntos.Mira la animación, y presta atención cuando se empiecen a mover los triángulos.
Quizás quieras verla varias veces para entender bien lo que pasa.
El triángulo violeta es el importante.
 |
se convierte en |  |
También tenemos una demostración sumando áreas.
| Nota histórica: aunque se llama Teorema de Pitágoras, ¡también lo conocían los matemáticos indios, griegos, chinos y babilonios antes de que él viviera! |
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).





