Longitud de Arco (Cálculo)
Uso del Cálculo para encontrar la longitud de
una curva.
(Por favor, lee primero sobre Derivadas
e Integrales).
Imagina que queremos encontrar la longitud de una curva entre dos puntos. Y la curva es suave (la derivada es continua).
Primero dividimos la curva en pequeñas longitudes y usamos la fórmula de Distancia entre dos puntos en cada longitud para obtener una respuesta aproximada:
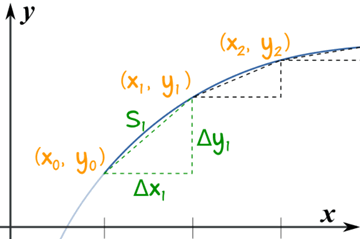
La distancia de x0 a x1 es:
S1 = √ (x1 − x0)2 + (y1 − y0)2
Y sea Δ (delta) la diferencia entre valores, de modo que tenemos:
S1 = √ (Δx1)2 + (Δy1)2
Ahora solo necesitamos muchos más segmentos:
S2 = √(Δx2)2 +
(Δy2)2
S3 = √(Δx3)2
+ (Δy3)2
...
...
Sn = √(Δxn)2
+ (Δyn)2
Podemos escribir todas esas líneas en una sola línea
usando una Suma:
¡Pero todavía estamos condenados a una gran cantidad de cálculos!
Tal vez podamos hacer una hoja de cálculo grande o escribir un
programa para hacer los cálculos ... pero intentemos algo más.
Tenemos un plan astuto:
- hagamos que todos los Δxi sean iguales para que podamos extraerlos del interior de la raíz cuadrada
- y luego convertir la suma en una integral.
Hagámoslo:
Primero, dividamos y multipliquemos Δyi por Δxi:
Ahora factorizamos (Δxi)2:
Sacamos (Δxi)2 de la raíz cuadrada:
Ahora, a medida que n tiende a infinito (a medida que nos dirigimos hacia un número infinito de cortes, y cada corte se vuelve más pequeño) obtenemos:
Ahora tenemos una integral y escribimos dx para indicar que los cortes Δx se acercan a un ancho cero (lo mismo para dy):
Y dy/dx es la derivada de la función f(x), que también se puede escribir f’(x):
La fórmula de Longitud de Arco
Y ahora, de repente, estamos en una posición mucho mejor, no
necesitamos sumar muchos cortes, podemos calcular una respuesta exacta
(si podemos resolver el diferencial y la integral).
Nota: la integral también funciona con respecto a y, útil si
conocemos x = g(y):
Así que los pasos a seguir son:
- Encontrar la derivada de f’(x)
- Resolver la integral de √1 + (f’(x))2 dx
Algunos ejemplos sencillos para empezar:
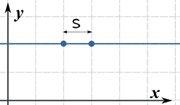
Ejemplo: Encuentra la longitud de f(x) = 2 entre x=2 y x=3
f(x) es solo una línea horizontal, por lo que su derivada es f’(x) = 0
Comienza con:
Pon f’(x) = 0:
Simplifica:
Calcula la Integral:
Entonces, la longitud del arco entre 2 y 3 es 1. Bueno, por
supuesto que lo es, ¡pero es bueno que hayamos encontrado la
respuesta correcta!
Punto interesante: la parte "(1 + ...)" de la fórmula de longitud
del arco garantiza que obtenemos al menos la
distancia entre los valores de x, como este caso donde f’(x)
es cero.

Ejemplo: Encuentra la longitud de f(x) = x entre x=2 y x=3
La derivada f’(x) = 1
Comienza con:
Pon f’(x) = 1:
Simplifica:
Y la diagonal a través de una unidad cuadrada es realmente la raíz cuadrada de 2, ¿verdad?
Bien, ahora las cosas más difíciles. Un ejemplo del mundo real.

Ejemplo: Se han instalado postes metálicos separados por
6m en un desfiladero.
Encuentra la longitud del puente colgante que sigue la curva:
f(x) = 5 cosh(x/5)
Aquí está la curva real:
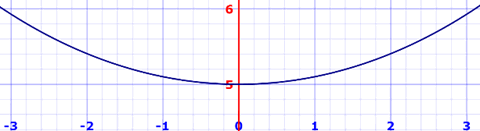
¡Resolvamos primero el caso general!
Un cable colgante forma una curva llamada catenaria:
f(x) = a cosh(x/a)
Los valores más grandes de a
tienen menos hundimiento en el medio
Y "cosh" es la función coseno
hiperbólico.
La derivada es f’(x) = sinh(x/a)
La curva es simétrica, por lo que es más fácil trabajar solo en la mitad de la catenaria, desde el centro hasta el final en "b":
Comienza con:
Pon f’(x) = sinh(x/a):
Usa la identidad 1 + sinh2(x/a) = cosh2(x/a):
Simplifica:
S = a sinh(b/a)
Ahora, recordando la simetría, vayamos de −b a +b:
S = 2a sinh(b/a)
En nuestro caso específico, a = 5 y el tramo de 6 m va de −3 a +3
S = 2×5 sinh(3/5)
= 6.367 m (redondeado a mm)
¡Es importante saberlo! Si lo construimos con una longitud de exactamente 6m, no habría forma de que podamos tirar de él con la fuerza suficiente para que entre en contacto con los postes. Pero a 6.367 m funcionará muy bien.
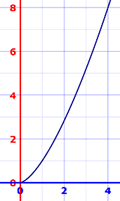
Ejemplo: Encuentra la longitud de y = x(3/2) de x = 0 a x = 4.
La derivada es y’ = (3/2)x(1/2)
Comienza con:
Pon (3/2)x(1/2):
Simplifica:
Podemos usar integración por sustitución:
- u = 1 + (9/4)x
- du = (9/4)dx
- (4/9)du = dx
- Límites: u(0)=1 y u(4)=10
Y nos queda:
Integra:
S = (8/27) u(3/2) de 1 a 10
Calcula:
S = (8/27) (10(3/2) − 1(3/2)) = 9.073...
Conclusión
La fórmula de longitud de arco para una función f(x) es:
Pasos:
- Calcula la derivada de f(x)
- Escribe la fórmula de longitud de arco
- Simplifica y resuelve la integral.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
