Separación de Variables
La Separación de Variables es un método especial para resolver algunas ecuaciones diferenciales
Una Ecuación Diferencial es una ecuación con una función y una o más de sus derivadas:
Ejemplo: una ecuación con la función y y su derivada dy dx
¿Cuándo se puede usar?
La separación de variables se puede utilizar cuando:
se pueden mover todos los términos y (incluido dy) a un lado
de la ecuación y
todos los términos x (incluido dx) al otro lado.
Método
Consiste en tres pasos:
- Paso 1 Mover todos los términos y (incluido dy) a un lado de la ecuación y todos los términos x (incluido dx) al otro lado.
- Paso 2 Integrar un lado con respecto a y y el otro lado con respecto a x. No olvides "+ C" (la constante de integración).
- Paso 3 Simplificar
Ejemplo: Resuelve esto (k es una constante):
dy dx = ky
Paso 1 Separa las variables moviendo todos los términos y a un lado de la ecuación y todos los términos x al otro lado:
Paso 2 Integra ambos lados de la ecuación por separado:
C es una constante de integración. Y usamos D para la otra, ya que es una constante diferente.
Paso 3 Simplifica:
La hemos resuelto:
y = cekx
Este es un tipo general de ecuación diferencial de primer orden que aparece en todo tipo de lugares inesperados en ejemplos del mundo real.
Usamos y y x, pero el mismo método funciona para otras letras como variables, como estas:

Ejemplo: ¡Conejos!
Cuantos más conejos adultos tengamos, más conejitos tendremos.¡Luego esos conejitos crecerán y también tendrán bebés! La población crecerá cada vez más rápido.
Las partes importantes de esto son:
- la población N en un tiempo t
- la tasa de crecimiento r
- la tasa de cambio de la población dNdt
dN dt = rN
¡Pero oye! ¡Es lo mismo que la ecuación que acabamos de resolver! Solo tiene letras diferentes:
- N en lugar de y
- t en lugar de x
- r en lugar de k
Entonces podemos saltar a la solución:
N = cert
Y aquí hay un ejemplo, la gráfica de N = 0.3e2t:
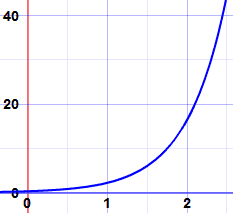
Crecimiento Exponencial
Hay otras ecuaciones que siguen este patrón, como la del interés compuesto continuamente.
Más Ejemplos
Bien, vamos a ver algunos ejemplos diferentes de separación de variables:
Ejemplo: Resuelve:
dydx = 1y
Paso 1 Separa las variables moviendo todos los términos y a un lado de la ecuación y todos los términos x al otro lado:
Paso 2 Integra ambos lados de la ecuación por separado:
Integramos ambos lados en un solo paso.
También usamos un atajo al usar solo una constante de integración C.
Esto es perfectamente válido ya que podríamos tener +D en una, +E en
la otra y simplemente decir que C = E−D.
Paso 3 Simplifica:
Nota: Esto no es lo mismo que y = √(2x) + C,
porque la C se agregó antes de sacar la raíz cuadrada. Esto sucede
mucho con las ecuaciones diferenciales. No podemos simplemente
agregar la C al final del proceso. Se agrega al hacer la
integración.
La hemos solucionado:
y = ±√(2(x + C))
Un ejemplo más difícil:
Ejemplo: Resuelve:
dydx = 2xy1+x2
Paso 1 Separa las variables:
Multiplica ambos lados por dx, divide ambos lados por y:
1y dy = 2x1+x2dx
Paso 2 Integra ambos lados de la ecuación por separado:
∫1y dy = ∫2x1+x2dx
El lado izquierdo es un logaritmo simple, y el lado derecho se puede integrar mediante sustitución:
Paso 3 Simplifica:
Ya es tan simple como puede ser. La hemos solucionado:
y = k(1 + x2)
Un ejemplo aún más difícil: la famosa Ecuación de Verhulst

Ejemplo: ¡Otra vez conejos!
Recordemos nuestra Ecuación Diferencial de crecimiento poblacional:
dNdt = rN
Bueno, ese crecimiento no puede continuar para siempre, ya que pronto se quedarían sin alimentos disponibles.
Un señor de apellido Verhulst incluyó una constante k (la población máxima que la comida puede soportar) para obtener:
dNdt = rN(1−N/k)
La Ecuación de Verhulst
¿Se puede solucionar esto?
Sí, con la ayuda de un truco...
Paso 1 Separa las variables:
Paso 2 Integra:
∫1N(1−N/k)dN = ∫ r dt
Hmmm ... el lado izquierdo parece difícil de integrar. De hecho, se puede hacer con un pequeño truco de Fracciones Parciales ... la reacomodamos así:
Ahora es mucho más fácil de resolver. Podemos integrar cada término por separado, así:
(¿Por qué eso se volvió menos ln(k−N)? Piénsalo por un segundo y recuerda que estamos integrando con respecto a N).
Paso 3 Simplifica:
¡Nos estamos acercando! Solo un poco más de álgebra para obtener N por separado:
Y tenemos la solución:
N = k1 + Ae−rt
Aquí hay un ejemplo, la gráfica de 401 + 5e−2t
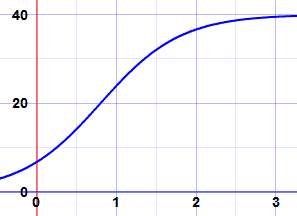
Empieza a subir exponencialmente
luego se aplana a medida que llega a k=40.
Cuán bonito.
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
