Qué es una función
Una función relaciona una entrada con una salida.
Una función es como una máquina: tiene una entrada y una salida.
Y lo que sale está relacionado de alguna manera con lo que entra.
| f(x) |
"f(x) = ... " es la forma clásica de escribir una
función. |
Entrada, relación, salida
Veremos muchas maneras de pensar en las funciones, pero siempre hay tres partes principales:- La entrada
- La relación
- La salida
Ejemplo: "Multiplicar por 2" es una función muy simple
Aquí están las tres partes:
| Entrada | Relación | Salida |
|---|---|---|
| 0 | × 2 | 0 |
| 1 | × 2 | 2 |
| 7 | × 2 | 14 |
| 10 | × 2 | 20 |
| ... | ... | ... |
Para una entrada de 50, ¿cuál es la salida?
Algunos ejemplos de funciones
- x2 (elevar al cuadrado) es una función
- x3+1 es también una función
- Seno, coseno y tangente son funciones utilizadas en la trigonometría
- ¡y hay muchas más!
Pero no vamos a mirar funciones específicas...
... en su lugar vamos a mirar la idea general de una
función.
Nombres
Primero, es útil darle un nombre a una función.
El nombre más común es "f", pero puedes ponerle otros como "g" ... o hasta "mermelada" si quieres.
Pero usemos "f":
Decimos "f de x es igual a x al cuadrado"
lo que entra en la función se pone entre paréntesis () después del nombre de la función:
Así que f(x) te dice que la función se llama "f", y "x" se pone dentro
Y normalmente verás lo que la función hace a la entrada:
f(x) = x2 nos dice que la función "f" toma "x" y lo eleva al cuadrado.
Ejemplo: con f(x) = x2:
- una entrada 4
- arroja un 16 como valor de salida.
De hecho, podemos escribir f(4) = 16.
La "x" es sólo un marcador de posición.
No te preocupes demasiado por la "x", solo está ahí para mostrarnos a dónde va la entrada y qué le pasa.¡Podría ser cualquier cosa!
Así que esta función:
f(x) = 1 - x + x2
es la misma función que:
- f(q) = 1 - q + q2
- h(A) = 1 - A + A2
- w(θ) = 1 - θ + θ2
La variable (x, q, A, etc.) está justo ahí para que sepamos dónde poner los valores:
f(2) = 1 - 2 + 22 = 3
A veces no hay nombre para la función
A veces una función no tiene nombre, y vemos algo como:
y = x2
Pero sigue habiendo:- una entrada (x)
- una relación (elevar al cuadrado)
- y una salida (y)
Relacionar
Arriba dije que una función es como una máquina. Pero una función no tiene engranajes ni correas ni partes que se muevan. ¡Y no destruye lo que pones dentro!
En realidad, una función relaciona la entrada con la salida.
Decir que "f(4) = 16" es como decir que 4 está relacionado de alguna manera con 16. O también 4 → 16

Ejemplo: este árbol crece 20 cm cada año, así que la altura del árbol está relacionada con la edad por la función a:
a(edad) = edad × 20
Así que si la edad es 10 años, la altura es a(10) = 200 cm
Aquí hay algunos valores de ejemplo:
| edad | a(edad) = edad× 20 |
|---|---|
| 0 | 0 |
| 1 | 20 |
| 3.2 | 64 |
| 15 | 300 |
| ... | ... |
¿Con qué tipo de cosas trabaja una función?
Los "números" parecen una respuesta clara, pero...
|
... ¿qué números?
Por ejemplo, la función de la
altura del árbol a(edad) = edad×20 no tiene
sentido si la edad es menor que cero.
|
... también podrían ser letras ("A"→"B"), o códigos de identificación ("A6309"→"Acceso") o cosas más raras. |
Así que tenemos que usar algo más general, y ahí es donde entran en juego los conjuntos:
Un conjunto es una colección de cosas, por ejemplo números.Aquí tienes algunos ejemplos:
|
Cada cosa individual en un conjunto (como "4" o "sombrero") es un miembro, o elemento.
Por lo tanto, una función toma elementos de un conjunto, y devuelve elementos de un conjunto.
Una función es especial
Pero una función tiene reglas especiales:- Debe funcionar para cada valor de entrada posible
- Y sólo tiene una relación por cada valor de entrada
Esto se puede decir en una definición:
Definición formal de función
¡Dos cosas importantes!
|
1. |
"...cada elemento..." de "X" se relaciona con un elemento de "Y". Decimos que la función cubre "X" (relaciona cada elemento de) (Pero algunos elementos de la Y podrían no estar relacionados en absoluto, lo cual está bien.) |
|
2. |
"...exactamente un elemento..." significa que la función es univaluada. No devolverá 2 o más resultados para la misma entrada. ¡Así que "f(2) = 7 o 9" no vale! |
|
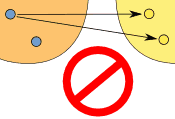
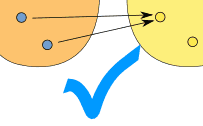
"Uno a muchos" no está permitido, pero "muchos a uno" sí: |
||
 |
 |
|
| (uno a muchos) | (muchos a uno) | |
| Esto NO está bien en una función | Pero esto SÍ está bien en una función | |
Cuando una relación no sigue esas dos reglas, entonces no es una función... sigue siendo una relación, pero no una función.
Ejemplo: La relación x → x2
También podría escribirse como una tabla:
| X: x | Y: x2 |
|---|---|
| 3 | 9 |
| 1 | 1 |
| 0 | 0 |
| 4 | 16 |
| -4 | 16 |
| ... | ... |
Es una función, porque:
- Cada elemento en X está relacionado con Y
- Ningún elemento en X tiene dos o más relaciones
(Fíjate en cómo tanto el 4 y el -4 se relacionan con el 16, lo cual está permitido.)
Ejemplo: Esta relación no es una función:
- El valor "3" en X no tiene relación en Y
- El valor "4" en X no tiene relación en Y
- El valor "5" está relacionado con más de un valor en Y
La prueba de la línea vertical
En un gráfico, la idea de univaluada significa que ninguna línea vertical cruza más de una vez.
Si alguna cruzara más de una vez no sería una función.
Algunos tipos de funciones tienen reglas más
estrictas, para saber más puedes leer Inyectiva,
suprayectiva y biyectiva
Infinitamente muchos
Los ejemplos que he mostrado tienen solo unos pocos valores, pero las funciones suelen trabajar en conjuntos de infinitos elementos.
Ejemplo: y = x3
- El conjunto de entrada "X" son todos los Números Reales
- El conjunto de salida "Y" es también todos los números reales
No podemos mostrar TODOS los valores, así que aquí hay algunos ejemplos:
| X: x | Y: x3 |
|---|---|
| -2 | -8 |
| -0.1 | -0.001 |
| 0 | 0 |
| 1.1 | 1.331 |
| 3 | 27 |
| etc. ... | etc. ... |
Dominio, codominio y rango
En el dibujo de arriba
- el conjunto "X" es el dominio,
- el conjunto "Y" es el codominio, y
- el conjunto de elementos de Y a los que llega alguna flecha (los valores verdaderos de la función) se llama rango o imagen.
Tenemos una página especial sobre dominio, codominio y rango por si quieres saber más.
¡Muchos nombres!
Las funciones se han utilizado en las matemáticas durante mucho tiempo, y han surgido muchos nombres y formas diferentes de escribir las funciones.Aquí hay algunos términos comunes con los que deberías familiarizarte:
Ejemplo: z = 2u3:
- "u" podría llamarse la "variable independiente"
- "z" podría llamarse la "variable dependiente" (depende del valor de u)
Ejemplo: f(4) = 16:
- "4" podría llamarse el "argumento"
- "16" podría llamarse el "valor de la función"
Ejemplo: h(año) = 20 × año:
- h() es la función
- "año" podría llamarse el "argumento", o la "variable"
- un valor fijo como "20" puede ser llamado un parámetro o constante
¡En computación, "año" sería el parámetro, y el valor que se le da a ese parámetro es la variable!
A menudo llamamos a una función "f(x)" cuando en realidad la función es realmente "f"
Pares ordenados
Y aquí hay otra forma de pensar en las funciones:
Puedes escribir las entradas y salidas de una función como "pares ordenados", como (4,16).
Se llaman pares ordenados porque la entrada siempre va primero y la salida después.
(entrada,salida)
Por lo que se ve así
( x,f(x) )
Ejemplo:
(4,16) significa que la función toma "4" y devuelve "16"
Conjunto de pares ordenados
Una función puede entonces definirse como un conjunto de pares ordenados:
Ejemplo: {(2,4), (3,5), (7,3)} es una función que dice:
"2 se relaciona con 4", "4 se relaciona con 5" y "7 se relaciona con 3".
También, fíjate en esto:- el dominio es {2,3,7} (los valores de entrada)
- y el rango es {4,5,3} (los valores de salida)
Pero la función debe ser univaluada, esto se puede decir
"si contiene (a, b) y (a, c), entonces b tiene que ser igual a c"
Es otra manera de decir que una entrada "a" no puede dar dos resultados diferentes.
Ejemplo: {(2,4), (2,5), (7,3)} no es una función porque {2,4} y {2,5} quieren decir que 2 estaría relacionado con 4 y 5.
O sea, no es función porque no es univaluada
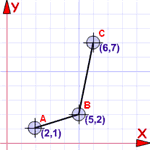
Un beneficio de los pares ordenados
¡Podemos graficarlos...
... porque también son coordenadas!
Así que un conjunto de coordenadas es también una función (si siguen las reglas anteriores, por supuesto)
Una función puede estar en pedazos
Podemos crear funciones que se comporten de manera diferente dependiendo del valor de entrada
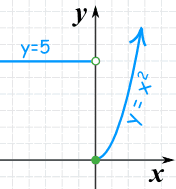
Ejemplo: Una función con dos partes:
- cuando x es menos de 0, da 5,
- cuando x es 0 o más da x2
 |
Aquí hay algunos valores de ejemplo:
|
Lee más en Función definida por partes.
Explícito vs. Implícito
Un último tema: los términos "explícito" e "implícito".Explícito es cuando la función nos muestra cómo ir directamente de x a y, como:
y = x3 − 3
Cuando conocemos x, podemos encontrar y
Es decir, el estilo clásico y = f(x) con
el que a menudo trabajamos.
Implícito es cuando no se da
directamente como:
x2 − 3xy + y3 = 0
Cuando conocemos x, ¿cómo encontramos y?
Puede ser difícil (¡o imposible!) ir directamente de la x a la y.
"Implícito" viene de "implícito", en otras palabras, mostrado indirectamente.
Graficadores
- El Graficador de funciones solo puede manejar funciones explícitas,
- El Graficador de ecuaciones puede manejar ambos tipos (pero toma un poco más de tiempo, y a veces se equivoca).
Conclusión
- una función relaciona entradas con salidas
- una función toma elementos de un conjunto (el dominio) y los relaciona con elementos de un conjunto (el codominio).
- las salidas (los verdaderos valores de la función) se llaman la imagen o rango
- una entrada sólo produce una salida (no una u otra)
- una función es un tipo especial de relación donde:
- cada elemento del dominio está incluido, y
- cualquier entrada produce solo una salida (no esto o aquello)
- una entrada y la salida que corresponde se llaman juntos un par ordenado
- así que una función también se puede ver como un conjunto de pares ordenados
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).