Distribución Binomial

"Bi" significa "dos" (como una bicicleta tiene dos ruedas) ... ... así que este tema se trata de cosas con dos resultados.

cara y cruz en una moneda de dólar

Lanzar una Moneda:

Podemos obtener Cara (C), o
Sello (S)

Y decimos que la probabilidad de que caiga C es ½
Y la probabilidad de que caiga S es ½

dado

Lanzar un Dado:

¿Cayó un 4 ... ?
... ¿o no?

Decimos que la probabilidad de un cuatro es 1/6 (una de las seis caras es un cuatro)
Y la probabilidad de no cuatro es 5/6 (cinco de las seis caras no son cuatro)

Ten en cuenta que un dado tiene 6 lados, pero aquí vemos solo dos casos: "cuatro: sí" o "cuatro: no"

¡Lancemos una moneda!

Lanza una moneda justa tres veces ... ¿cuál es la posibilidad de obtener dos caras?

Al lanzar una moneda tres veces (C es para cara, S para sello) se pueden obtener cualquiera de estos 8 resultados:

CCC
CCS
CSC
CSS
SCC
SCS
SSC
SSS

¿Qué resultados queremos?

"Dos Caras" pueden estar en cualquier orden: "CCS", "SCC" y "CSC" tienen dos caras (y un sello).

Entonces 3 de los resultados tienen "dos caras".

¿Cuál es la probabilidad de cada resultado?

Cada resultado es igualmente probable, y hay 8 de ellos, por lo que cada resultado tiene una probabilidad de 1/8

Así que la probabilidad del evento "Dos Caras" es:

Número de resultados que queremos		Probabilidad de cada resultado
3	×	1/8	= 3/8

Entonces la probabilidad de conseguir Dos Caras es 3/8

Usamos estas palabras especiales:

Resultado: es cualquier resultado de los tres lanzamientos de la moneda (8 posibilidades diferentes)
Evento: "Dos Caras" es un evento posible de tres lanzamientos de una moneda (y vimos que 3 resultados tienen esto)

3 Caras, 2 Caras, 1 Cara, Ninguna

Los cálculos son (P significa "Probabilidad de"):

P(Tres Caras) = P(CCC) = 1/8
P(Dos Caras) = P(CCS) + P(CSC) + P(SCC) = 1/8 + 1/8 + 1/8 = 3/8
P(Una Cara) = P(CSS) + P(SCS) + P(SSC) = 1/8 + 1/8 + 1/8 = 3/8
P(Cero Caras) = P(SSS) = 1/8

Podemos escribir esto en términos de una Variable Aleatoria, X, = "El número de Caras de 3 lanzamientos de una moneda":

P(X = 3) = 1/8
P(X = 2) = 3/8
P(X = 1) = 3/8
P(X = 0) = 1/8

Y así es como se ve en una Gráfica de Barras:

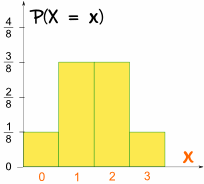
binomial 1
¡Es simétrica!

Elaborando una fórmula

Ahora imagina que queremos las posibilidades de 5 caras en 9 lanzamientos: ¡enumerar los 512 resultados llevará mucho tiempo!

Entonces hagamos una fórmula.

En nuestro ejemplo anterior, ¿cómo podemos obtener los valores 1, 3, 3 y 1?

Triángulo de Pascal

Bueno, ¡en realidad están en el Triángulo de Pascal!

¿Podemos obtenerlos usando una fórmula?

Claro que podemos, y aquí está:

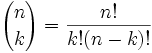
binomial n en k = n! / k!(n-k)!

Con frecuencia se le llama "n en k"

n = número total
k = número que queremos

El "!" significa "factorial, por ejemplo", 4! = 1×2×3×4 = 24

Nota: a menudo se le llama "n en k" y puedes obtener más información aquí.

Pongamos a prueba la fórmula.

Ejemplo: con 3 lanzamientos, ¿cuáles son las probabilidades de 2 Caras?

Tenemos n=3 y k=2:

n!k!(n-k)! =3!2!(3-2)!

=3×2×12×1 × 1

= 3

Entonces hay 3 resultados que tienen "2 Caras"

(Ya lo sabíamos, pero ahora tenemos una fórmula para ello).

Usémosla para una pregunta más difícil:

Ejemplo: con 9 lanzamientos, ¿cuáles son las probabilidades de 5 Caras?

Tenemos n=9 y k=5:

n!k!(n-k)! =9!5!(9-5)!

=9×8×7×6×5×4×3×2×15×4×3×2×1 × 4×3×2×1

=126

Entonces 126 de los resultados tendrán 5 cabezas

Y para 9 lanzamientos hay un total de 2⁹ = 512 resultados, por lo que obtenemos la probabilidad:

Número de resultados que queremos		Probabilidad de cada resultado
126	×	1/512	= 126/512

Entonces:

P(X=5) = 126512 = 0.24609375

Aproximadamente una probabilidad del 25%.

(Más fácil que enumerarlas todas).

Sesgos

Hasta ahora, las probabilidades de éxito o fracaso han sido igualmente probables.

Pero, ¿qué pasa si las monedas están sesgadas (aterrizan más de un lado que del otro) o las opciones no son 50/50.

Ejemplo: Vendes sándwiches. El 70% de las personas elige pollo, el resto elige otra cosa.

¿Cuál es la probabilidad de vender exactamente a 2 de los siguientes 3 clientes sándwiches de pollo?

Esto es como el ejemplo de cara y sello, pero con 70/30 en lugar de 50/50.

Dibujemos un diagrama de árbol:

diagrama de árbol pollo

Los casos donde ocurren "Dos Pollos" están resaltados.

Las probabilidades para "Dos Pollos" resultan ser 0.147, porque estamos multiplicando dos 0.7s y un 0.3 en cada caso. En otras palabras:

0.147 = 0.7 × 0.7 × 0.3

O, usando exponentes:

= 0.7² × 0.3¹

El 0.7 es la probabilidad de cada opción que queremos, llamémosla p

El 2 es la cantidad de opciones que queremos, llamémosle k

Y tenemos (hasta ahora):

= p^k × 0.3¹

El 0.3 es la probabilidad de la opción opuesta, entonces es: 1−p

El 1 es el número de opciones opuestas, por lo que es: n−k

Lo cual nos da:

= p^k(1-p)^(n-k)

Donde

p es la probabilidad de cada opción que queremos
k es la cantidad de opciones que queremos
n es el número total de opciones

Ejemplo: (continuación)

p = 0.7 (probabilidad de que elijan pollo)
k = 2 (cantidad de elecciones de pollo que queremos)
n = 3 (número total de elecciones, una por cada cliente)

Así que tenemos:

p^k(1-p)^(n-k) =0.7²(1-0.7)^(3-2)

=0.7²(0.3)⁽¹⁾

=0.7 × 0.7 × 0.3

=0.147

que es lo que obtuvimos antes, pero ahora usando una fórmula

Ahora sabemos que la probabilidad de cada resultado es 0.147

Pero debemos incluir que hay tres formas en que puede suceder: (pollo, pollo, otro) o (pollo, otro, pollo) o (otro, pollo, pollo)

Ejemplo: (continuación)

El número total de resultados de "dos pollos" es:

n!k!(n-k)! =3!2!(3-2)!

=3×2×12×1 × 1

Y tenemos:

Número de resultados que queremos		Probabilidad de cada resultado
3	×	0.147	=	0.441

Entonces, la probabilidad del evento "2 personas de cada 3 eligen pollo" = 0.441

Okay. Eso fue mucho trabajo para algo que ya sabíamos, pero ahora tenemos una fórmula que podemos usar para preguntas más difíciles.

Ejemplo: Lucas dice "70% elige pollo, por lo que 7 de los siguientes 10 clientes deberían elegir pollo" ... ¿cuál es la probabilidad de que Lucas tenga razón?

Tenemos:

p = 0.7
n = 10
k = 7

Y obtenemos:

p^k(1-p)^(n-k) =0.7⁷(1-0.7)^(10-7)

=0.7⁷(0.3)⁽³⁾

=0.0022235661

Esa es la probabilidad de cada resultado.

Y el número total de esos resultados es:

n!k!(n-k)! =10!7!(10-7)!

=10×9×8×7×6×5×4×3×2×17×6×5×4×3×2×1 × 3×2×1

=10×9×83×2×1

=120

Finalmente:

Número de resultados que queremos		Probabilidad de cada resultado
120	×	0.0022235661	=	0.266827932

Entonces, la probabilidad de que 7 de cada 10 elijan pollo es aproximadamente 27%

Moraleja de la historia: a pesar de que el promedio a largo plazo es del 70%, no esperes 7 de los próximos 10.

Todo junto

Ahora sabemos cómo calcular cuántos:

n!k!(n-k)!

Y la probabilidad de cada uno:

p^k(1-p)^(n-k)

Cuando se multiplican juntos obtenemos:

Probabilidad de k de un total de n maneras:

P(k de n) = n!k!(n-k)! p^k(1-p)^(n-k)

La Fórmula General de Probabilidad Binomial

Notas importantes:

Los sucesos son independientes,
Solo hay dos resultados posibles en cada evento,
La probabilidad de "éxito" en cada evento es constante.

Quincunce

Juega con el Quincunce (luego lee Quincunce Explicado) para ver la Distribución Binomial en acción.

Lanza el dado

dado

Se lanza un dado justo cuatro veces. Calcule las probabilidades de obtener:

0 Dos
1 Dos
2 Dos
3 Dos
4 Dos

En este caso n=4, p = P(Dos) = 1/6

X es la variable aleatoria "Número de 2's en cuatro lanzamientos".

Sustituye x = 0 a 4 en la fórmula:

P(k de n) = n!k!(n-k)! p^k(1-p)^(n-k)

Así (a 4 decimales):

P(X = 0) = 4!0!4! × (1/6)⁰(5/6)⁴ = 1 × 1 × (5/6)⁴ = 0.4823
P(X = 1) = 4!1!3! × (1/6)¹(5/6)³ = 4 × (1/6) × (5/6)³ = 0.3858
P(X = 2) = 4!2!2! × (1/6)²(5/6)² = 6 × (1/6)² × (5/6)² = 0.1157
P(X = 3) = 4!3!1! × (1/6)³(5/6)¹ = 4 × (1/6)³ × (5/6) = 0.0154
P(X = 4) = 4!4!0! × (1/6)⁴(5/6)⁰ = 1 × (1/6)⁴ × 1 = 0.0008

Resumen: "para los 4 lanzamientos, hay un 48% de probabilidades de que no haya dos, 39% de 1 dos, 12% de 2, 1.5% de 3 y tan solo 0.08% de que todos los lanzamientos sean un dos (¡pero aún podría suceder!)"

Esta vez la Gráfica de Barras no es simétrica:

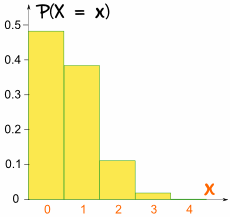
binomial 0 a 4 asimétrico
¡No es simétrica!

Es asimétrica porque p es diferente de 0.5

bicicleta

Bicicletas de montaña

Tu empresa fabrica bicicletas de montaña. El 90% pasa la inspección final (y el 10% falla y debe repararse).

¿Cuáles son los valores esperados para la Media y la Varianza de las siguientes 4 inspecciones?

Primero, calculemos todas las probabilidades.

n = 4,
p = P(Pasa) = 0.9

X es la variable aleatoria "Número de bicicletas que pasan la prueba en las cuatro inspecciones".

Sustituye x = 0 a 4 en la fórmula:

P(k de n) = n!k!(n-k)! p^k(1-p)^(n-k)

Así:

P(X = 0) = 4!0!4! × 0.9⁰0.1⁴ = 1 × 1 × 0.0001 = 0.0001
P(X = 1) = 4!1!3! × 0.9¹0.1³ = 4 × 0.9 × 0.001 = 0.0036
P(X = 2) = 4!2!2! × 0.9²0.1² = 6 × 0.81 × 0.01 = 0.0486
P(X = 3) = 4!3!1! × 0.9³0.1¹ = 4 × 0.729 × 0.1 = 0.2916
P(X = 4) = 4!4!0! × 0.9⁴0.1⁰ = 1 × 0.6561 × 1 = 0.6561

Resumen: "para las 4 próximas bicicletas, hay una pequeña probabilidad de 0.01% de que ninguna pase la inspección, 0.36% de probabilidad de 1 pase, 5% de probabilidad de 2 pases, 29% de probabilidad de 3 pases y una enorme probabilidad de 66% de que todas pasen la inspección".

Media, varianza y desviación estándar

Calculemos la Media, Varianza y Desviación Estándar para las inspecciones de bicicletas de montaña.

Hay fórmulas (relativamente) simples para ello. Son un poco difíciles de demostrar, ¡pero funcionan!

La media, o "valor esperado", es:

μ = np

Para las bicicletas de montaña:

μ = 4 × 0.9 = 3.6

Por lo tanto, podemos esperar que 3.6 bicicletas (de 4) pasen la inspección.
Realmente tiene sentido ... 0.9 de probabilidad por cada bicicleta multiplicada por 4 bicicletas es igual a 3.6

La fórmula para la varianza es:

Varianza: σ² = np(1-p)

Y la desviación estándar es la raíz cuadrada de la varianza:

σ = √[np(1-p)]

Para las bicicletas de montaña:

Varianza: σ² = 4 × 0.9 × 0.1 = 0.36

La desviación estándar es:

σ = √(0.36) = 0.6

Nota: también podríamos calcular todo manualmente, haciendo una tabla como esta:

X	P(X)	X × P(X)	X² × P(X)
0	0.0001	0	0
1	0.0036	0.0036	0.0036
2	0.0486	0.0972	0.1944
3	0.2916	0.8748	2.6244
4	0.6561	2.6244	10.4976
	SUMA:	3.6	13.32

La media es la Suma de (X × P(X)):

μ = 3.6

La varianza es la Suma de (X² × P(X)) menos Media²:

Varianza: σ² = 13.32 − 3.6² = 0.36

La desviación estándar es:

σ = √(0.36) = 0.6

Y obtuvimos los mismos resultados que antes (¡genial!)

Resumen

La Fórmula General de Probabilidad Binomial:
P(k de n) = n!k!(n-k)! p^k(1-p)^(n-k)
Media de X: μ = np
Varianza de X: σ² = np(1-p)
Desviación estándar de X: σ = √[np(1-p)]

¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).

Question 1 Question 2 Question 3 Question 4 Question 5 Question 6 Question 7 Question 8 Question 9 Question 10 Question 11 Question 12