Teoremas Sobre Triángulos Semejantes
1. Teorema de Proporcionalidad de Tales
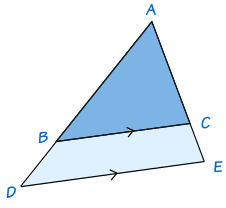
Si ADE es cualquier triángulo y BC se dibuja paralela a DE, entonces ABBD = ACCE
Para demostrar que esto es cierto, dibuja la línea BF paralela a AE para completar un paralelogramo BCEF:
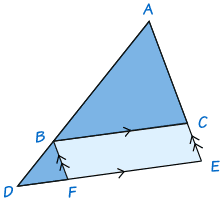
Los triángulos ABC y BDF tienen exactamente los mismos ángulos y, por lo tanto, son semejantes (¿Por qué? Mira la sección llamada AA en la página Cómo Saber si Dos Triángulos Son Semejantes.)
- El lado AB corresponde al lado BD y el lado AC corresponde al lado BF.
- Por lo tanto, AB/BD = AC/BF
- Pero BF = CE
- Por lo tanto, AB/BD = AC/CE
Teorema de la Bisectriz
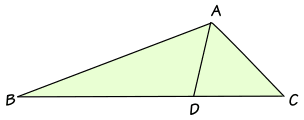
Si ABC es cualquier triángulo y AD biseca (corta a la mitad) el ángulo BAC, entonces ABBD = ACDC
Para demostrar que esto es cierto, podemos etiquetar el triángulo así:
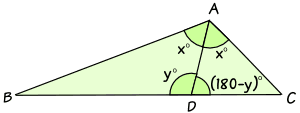
- Ángulo BAD = Ángulo DAC = x°
- Ángulo ADB = y°
- Ángulo ADC = (180−y)°
Tanto ABBD como ACDC son iguales a sen(y)sen(x), por lo tanto:
ABBD = ACDC
En particular, si el triángulo ABC es isósceles, entonces los triángulos ABD y ACD son triángulos congruentes
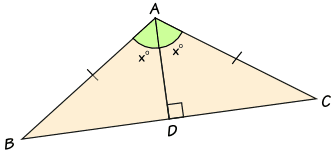
Y el mismo resultado es cierto:
ABBD = ACDC
3. Área y similitud
Si dos triángulos semejantes tienen
lados en la razón x:y,
entonces sus áreas están en la proporción x2:y2
Ejemplo:
Estos dos triángulos son semejantes con lados en la proporción 2:1 (los lados de uno son el doble de largos que los del otro):

La respuesta es simple si solo dibujamos tres líneas más:
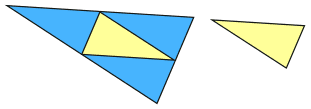
Por lo tanto, cuando las longitudes son el doble de largas, el área es cuatro veces más grande.
Por lo tanto, la proporción de sus áreas es 4:1
También podemos escribir 4:1 como 22:1
El caso general:
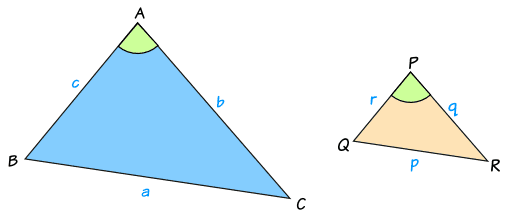
Los triángulos ABC y PQR son semejantes y tienen lados en la proporción x:y
Podemos encontrar las áreas usando esta fórmula para el Área de un Triángulo:
Área de ABC = 12bc sen(A)
Área de PQR = 12qr sen(P)
Y sabemos que las longitudes de los triángulos están en la proporción x:y
q/b = y/x, luego: q = by/x
y r/c = y/x, luego r = cy/x
Además, dado que los triángulos son semejantes, los ángulos A y P son iguales:
A = P
Ahora podemos hacer algunos cálculos:
Por lo tanto, terminamos con esta relación:
Área del Triángulo ABC : Área del Triángulo PQR = x2 : y2
¡Refuerza tu aprendizaje resolviendo los siguientes retos sobre este tema! (Nota: están en inglés).
