Completar el Cuadrado

"Completar el cuadrado" es cuando...

... tenemos una ecuación cuadrática como:		y la ponemos en esta forma:
ax² + bx + c = 0		a(x+d)² + e = 0

Si tienes prisa, puedo decirte de una vez que: d = b2a

y: e = c − b²4a

Pero si tienes tiempo, deja que te explique cómo "Completar el Cuadrado" por tu cuenta.

Completar el Cuadrado

Supongamos que tenemos una expresión sencilla como x² + bx. Tener x dos veces en la misma expresión puede complicarnos la vida. ¿Qué podemos hacer?

Bueno, con un poco de inspiración geométrica podemos convertir la expresión, de la siguiente forma:

Completando el cuadrado geométricamente

Como puedes ver x² + bx puede ser reacomodado casi en un cuadrado...

... y podemos completar el cuadrado con (b/2)²

Algebraicamente se ve de esta forma:

x² + bx	+ (b/2)²	=	(x+b/2)²
	"Completar el Cuadrado"

Entonces, si sumamos (b/2)² podemos completar el cuadrado.

Y (x+b/2)² tiene una sola x, lo cual es más fácil de usar.

Manteniendo el balance

Ahora... ¡No podemos simplemente sumar (b/2)² sin restarlo también! De lo contrario toda la expresión cambiaría.

Veamos cómo hacer esto de forma correcta mediante un ejemplo:

Empieza con:
	("b" es 6 en este caso)

Completa el Cuadrado:
	También resta el nuevo término
Simplifícalo y listo.

El resultado:

x² + 6x + 7 = (x+3)² − 2

Y ahora la x aparece una sola vez, ¡y nuestro trabajo ha terminado!

Un Camino Más Corto

Veamos una manera más rápida de obtener la respuesta. Puede que te guste este método.

Primero piensa en el resultado que queremos: (x+d)² + e

Después de desarrollar (x+d)² obtenemos: x² + 2dx + d² + e

Ahora intenta convertir nuestro ejemplo en esa forma para encontrar d y e.

Ejemplo: Intenta escribir x² + 6x + 7 de forma x² + 2dx + d² + e

x^2 + (6x) + [7] se iguala con x^2 + (2dx) + [d^2+e]

Ahora podemos "forzar" una respuesta:

Sabemos que 6x debe terminar como 2dx, por lo que d debe ser 3
Luego vemos que el 7 debe convertirse en d² + e = 9 + e, por lo que e debe ser −2

¡Y obtenemos el mismo resultado (x+3)² − 2 que antes!

A continuación veamos una aplicación de todo esto: resolver Ecuaciones Cuadráticas ...

Resolviendo Ecuaciones Cuadráticas Completando el Cuadrado

Podemos completar el cuadrado para resolver una Ecuación Cuadrática (hallar los valores para los cuales es igual a cero).

Pero una Ecuación Cuadrática en forma general puede tener un coeficiente de valor a en frente de x²:

ax² + bx + c = 0

Pero eso es fácil de arreglar... tan solo divide toda la ecuación por "a", luego continúa:

x² + (b/a)x + c/a = 0

Pasos a seguir

Ahora podemos resolver una Ecuación Cuadrática en 5 pasos:

Paso 1 Divide todos los términos por a (el coeficiente de x²).
Paso 2 Mueve el término numérico (c/a) al lado derecho de la ecuación.
Paso 3 Completa el cuadrado del lado izquierdo de la ecuación y mantén el balance sumando el mismo valor del lado derecho de la ecuación.

Ahora tenemos algo que se ve como (x + p)² = q, lo cuál se puede solucionar fácilmente:

Paso 4 Aplica la raíz cuadrada en ambos lados de la ecuación.

Paso 5 Resta el número que queda del lado izquierdo para hallar el valor de x.

Ejemplos

OK, ¡algunos ejemplos serán de ayuda!

Ejemplo 1: Resuelve x² + 4x + 1 = 0

Paso 1 Podemos omitir este paso porque el coeficiente de x² es 1

Paso 2 Mueve la constante al lado derecho de la ecuación:

x² + 4x = -1

Paso 3 Completa el cuadrado del lado izquierdo de la ecuación y mantén el balance sumando el mismo número del lado derecho de la ecuación.

(b/2)² = (4/2)² = 2² = 4

x² + 4x + 4 = -1 + 4

(x + 2)² = 3

Paso 4 Aplica la raíz cuadrada en ambos lados:

x + 2 = ±√3 = ±1.73 (a 2 decimales)

Paso 5 Resta 2 de ambos lados:

x = ±1.73 – 2 = -3.73 ó -0.27

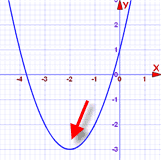
Veamos un dato interesante y útil.

Después del Paso 3 teníamos la ecuación:

(x + 2)² = 3

La cual nos indica el vértice (punto de giro) de x² + 4x + 1: (-2, -3)

Ejemplo 2: Resuelve 5x² – 4x – 2 = 0

Paso 1 Divide todos los términos por 5

x² – 0.8x – 0.4 = 0

Paso 2 Mueve la constante hacia el lado derecho de la ecuación:

x² – 0.8x = 0.4

Paso 3 Completa el cuadrado del lado izquierdo de la ecuación y mantén el balance sumando el mismo número del lado derecho de la ecuación.

(b/2)² = (0.8/2)² = 0.4² = 0.16

x² – 0.8x + 0.16 = 0.4 + 0.16

(x – 0.4)² = 0.56

Paso 4 Aplica la raíz cuadrada en ambos lados:

x – 0.4 = ±√0.56 = ±0.748 (a 3 decimales)

Paso 5 Resta (-0.4) de ambos lados (en otras palabras, suma 0.4):

x = ±0.748 + 0.4 = -0.348 ó 1.148

¿Para qué "completar el cuadrado"?

¿Para qué querrías completar el cuadrado cuando basta usar la fórmula cuadrática para resolver una ecuación cuadrática?

Bueno, la respuesta está arriba, en parte, donde la forma nueva te da el vértice, y también hace la ecuación fácil de resolver.

A veces la forma ax² + bx + c puede ser parte de un problema más grande y escribirla como a(x+d)² + e hace más fácil llegar a la solución, porque la x solo aparece una vez.

Por ejemplo, "x" puede ser una función (como cos(z)) y reescribir puede abrirte un mejor camino hacia la solución.

Además, Completar el Cuadrado es el primer paso en la derivación de la fórmula cuadrática

Simplemente piensa que es otra herramienta en tu caja de herramientas matemáticas.

¡Intenta resolver las siguientes preguntas sobre este tema! (Nota: están en inglés).

Nota: Valores de "d" y "e"

¿Cómo obtuve los valores de d y e de la parte superior de la página?

Empieza con	$ecuación cuadrática$
Divide la ecuación por a	$ecuación cuadrática_2$
Pon c/a del otro lado	$ecuación cuadrática_3$
Suma (b/2a)² a ambos lados

"Completa el Cuadrado"
Ahora trae todo de vuelta...
... al lado izquierdo	$ecuación cuadrática_6$
... y multiplica por el coeficiente inicial a de x²	$ecuación cuadrática_7$