Interés compuesto

A lo mejor quieres leer primero la Introducción al interés

Para el interés compuesto, calculamos el interés del primer periodo, lo sumamos al total, y después calculamos el interés del siguiente periodo, y sigue... así:

Aquí tienes los cálculos para un préstamo de 5 años al 10%:

Como ves, es fácil calcular si vas paso a paso.

1. Calcula el interés (= "préstamo inicial" × tasa de interés)
2. Suma el interés al "préstamo inicial" para calcular el "préstamo final" del año
3. El "préstamo final" del año es el "préstamo inicial" del año siguiente

Una tarea simple, con muchos cálculos. Pero hay maneras más rápidas, siendo listos con las matemáticas.

Hagamos una fórmula

Vamos a hacer una fórmula para lo de arriba... empezamos mirando el primer año:

$1,000.00 + ($1,000.00 × 10%) = $1,100.00

Lo podemos reescribir así:

Así que sumar el 10% de interés es como multiplicar por 1.10

Nota: la tasa de interés la hemos escrito en decimal dividiendo entre 100: 10% = 10/100 = 0.10, lee Porcentajes para saber más.

Así que ahora es todo en un paso:

1. Multiplica el "préstamo inicial" por (1 + tasa de interés) para calcular el "préstamo final"

(¡Pero recuerda que primero hay que poner la tasa de interés en decimal! 0.10, no 10%)

Con un simple cálculo vemos que el resultado es el mismo:

Ahora viene la magia...

... ¡la misma fórmula vale todos los años!

· Podemos calcular el año siguiente así: $1,100 × 1.10 = $1,210
· Y seguimos otro año más: $1,210 × 1.10 = $1,331
· etc...

Así es como funciona:

De hecho podemos ir directamente desde el principio hasta el año 5, multiplicando 5 veces:

$1,000 × 1.10 × 1.10 × 1.10 × 1.10 × 1.10 = $1,610.51

Pero es más fácil escribir las multiplicaciones usando exponentes (o potencias) así:

La fórmula

Hemos usado un ejemplo real, pero podemos hacerlo en general con letras en vez de números, así:

(¿Ves que es lo mismo? Antes teníamos PV = $1,000, r = 0.10, n = 5, y FV = $1,610.51)

Esta es la fórmula básica para el interés compuesto. Apréndetela, es muy útil.

Ejemplos

¿Qué tal unos ejemplos...?

¿Y si el préstamo fuera de 15 años? ... sólo tienes que cambiar el valor de "n":

... ¿y si el préstamo fuera de 5 años, pero la tasa de interés fuera sólo del 6%? Queda así:

¿Has visto cómo hemos puesto el 6% en su sitio?

... ¿ y si fuera de 20 años al 8%? ... ¡esa la calculas tú!

Calcular "al revés" para encontrar el valor presente

Digamos que tu objetivo es tener $2,000 dentro de 5 años. Te dan un 10% en el banco, así que ¿cuánto tienes que poner al principio?

Es decir, conoces el valor futuro, y quieres conocer el valor presente.

Sabemos que si multiplicamos un valor presente (PV) por (1+r)ⁿ nos da el valor futuro (FV), así que podemos volver atrás dividiendo:

Así que la fórmula es:

PV = FV / (1+r)ⁿ

Y podemos calcular la respuesta del problema:

PV = $2,000 / (1+0.10)⁵ = $2,000 / 1.61051 = $1,241.84

O sea, $1,241.84 crecerán hasta $2,000 si los invertimos al 10% durante 5 años.

Periodos de interés compuesto

El interés compuesto no se calcula siempre por año, puede ser al mes, al día, etc. ¡Pero si no es anual deberían decirlo!

También se puede tener interés anual pero varias veces en el mismo año, lo que se llama Composición periódica.

¡Así que ten cuidado con los significados!

TAE

	Como es fácil confundirse cuando lees un anuncio (¡a veces lo hacen a propósito!), se suele usar el "TAE". TAE quiere decir "Tasa Anual Equivalente" ... te dice lo que vas a sacar en realidad cada año (incluyendo el compuesto, costes, etc.)
En este anuncio parece que es 6.25%, pero en realidad es 6.335%

Aquí hay más ejemplos:

Y:

Si estás buscando hacer negocios, pregunta por el TAE.

¡Un respiro!

Hasta ahora hemos usado (1+r)ⁿ para ir de un valor presente (PV) a un valor futuro (FV) y al revés, además hemos visto algunos de los trucos que te puedes encontrar en un préstamo.

Ahora tómate un descanso antes de seguir con los dos temas siguientes:

• Cómo calcular la tasa de interés si conoces el PV, el FV y el número de periodos
• Cómo calcular el número de periodos si conocemos el PV, el FV y la tasa de interés

Calcular la tasa de interés

Puedes calcular la tasa de interés si sabes el valor presente, el valor futuro y cuántos periodos son.

Ejemplo: tienes $1,000, y quieres tener $2,000 en 5 años, ¿qué tasa de interés te hace falta?

La fórmula es:

r = ( FV / PV )^1/n - 1

Nota: el pequeño "1/n" es un exponente fraccionario, primero calcula 1/n y luego úsalo como exponente en la calculadora. Por ejemplo 20.2 lo calcularíamos así: 2, "x^y", 0, ., 2, =

Ahora "metemos" los valores para tener el resultado:

r = ( $2,000 / $1,000 )^1/5 - 1 = ( 2 )^0.2 - 1 = 1.1487 - 1 = 0.1487

Y 0.1487 en porcentaje es 14.87%,

Así que te haría falta una tasa de interés del 14.87% para que $1,000 se convirtieran en $2,000 en 5 años.

Calcular el número de periodos

Puedes calcular cuántos periodos son si sabes el valor presente, el valor futuro y la tasa de interés.

Ejemplo: quieres saber cuántos periodos necesitas para que tus $1,000 se conviertan en $2,000 al 10% de interés.

Esta es la fórmula (nota: usa el logaritmo natural ln):

n = ln(FV / PV) / ln(1 + r)

La función "ln" debería de estar en tu calculadora si es de las buenas. También hay log, no las confundas.

En fin, vamos a "meter" los valores:

n = ln( $2,000 / $1,000 ) / ln( 1 + 0.10 ) = ln(2)/ln(1.10) = 0.69315/0.09531 = 7.27

¡Magia! Dentro de 7.27 años tus $1,000 serán $2,000 al 10% de interés.

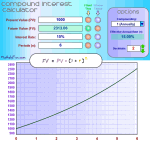Calculadora

He hecho una Calculadora de interés compuesto que usa estas fórmulas, por si te interesa.

Resumen

La fórmula básica para el interés compuesto es:

Anualidades

Hasta ahora hemos hablado de lo que pasa con una cantidad cuando el tiempo va pasando... ¿pero qué pasa si tienes una serie de cantidades, como pagos periódicos de un préstamo o inversiones anuales? De esto hablamos en la página de Anualidades, pronto la tendremos lista.